Especial IV Premios ACE (IX) | Proyecto «Diseño de anillos de compresión no circulares y distribución óptima de fuerzas en el plano»

Repaso a las candidaturas recibidas en la IV edición de los Premios ACE

A lo largo de las últimas semanas, se han presentado todas las candidaturas correspondientes a las categorías Mejor Obra de Estructura y Mejor Obra de Estructura Pequeña de los IV Premios ACE. En este caso, os ofrecemos el proyecto ganador de la categoría Mejor Trabajo de Investigación, de Estudio o Informe. Recibe el título de «Diseño de anillos de compresión no circulares y distribución óptima de fuerzas en el plano«.

Es la tesis doctoral de Rodrigo Martín Sáiz. Fue dirigida por el profesor Ramon Sastre. Su defensa tuvo lugar el 18 de diciembre de 2015 en el salón de actos de la Escuela Técnica Superior de Arquitectura del Vallès. Obtuvo una calificación de sobresaliente cum laude.

Fue la única candidatura recibida dentro de su categoría. El jurado tenía la opción de dejar vacante el galardón, pero decidió conceder el reconocimiento al trabajo que analizaremos a continuación:

TEMÁTICA:

La investigación se encuadra dentro del área tecnológica de la ingeniería estructural en la arquitectura, más concretamente, en el diseño de estructuras tensadas de cubierta con grandes luces. Se fundamenta en la necesidad de profundizar en uno de los mayores problemas que tienen que resolverse en los proyectos de este tipo de cubiertas: el equilibrio de las reacciones que generan sus fuerzas internas, de tracción y sensiblemente horizontales.

Este equilibro se debe conseguir muchas veces de manera autónoma, es decir, no con anclajes al terreno o a grandes cimentaciones, sino mediante elementos rígidos equilibrantes dentro de la propia estructura.

La tesis se centra en los anillos de compresión por ser los elementos equilibrantes más recurrentes y susceptibles de ser optimizados. Se estudian alternativas a los anillos de planta circular, que se adapten mejor a la diversidad e irregularidad de la geometría en planta de los edificios sobre los que se construyen estas cubiertas, pero aproximando su eficiencia estructural a la que resulta en los anillos circulares.

APORTACIÓN:

Nuevos conocimientos sobre el diseño de anillos de compresión con geometrías no circulares basado en criterios de optimización para su dimensionado.

APLICABILIDAD:

No es una investigación cerrada en sí misma, ya que sólo plantea resolver una parte de un proceso de diseño más complejo: la geometría no circular del anillo de compresión y la distribución óptima de fuerzas en su plano. Sin embargo, sus conclusiones son ya de aplicación en los diseños estructurales donde, además de ligereza y autonomía, se imponga una condición de no circularidad de su perímetro; principalmente, en el planteamiento de cubiertas tensadas de grandes luces de planta no circular para estadios, centros deportivos, patios de edificios históricos, plazas públicas, etc. Aunque también en el diseño de otros artefactos que tengan esas mismas condiciones de diseño.

RELEVANCIA:

Esta investigación ha dado lugar, además, a varias publicaciones del mismo autor en forma de artículo científico-técnico:

•  “Composition of Non-circular Compression Rings with Optimal Behaviour in Radial Tensile Roofs”. Publicado en la revista Archi-DOCT. The e-journal for the dissemination of doctoral research in architecture.
• “Distribución Óptima de Fuerzas en el Plano de Anillos de Compresión de Planta Elíptica”. Publicado después de la lectura de la tesis en Quaderns d’Estructures de la Associació de Consultorsd’Estructures.
• “Dos estructuras tipo rueda de bicibleta de planta elíptica”. Artículo en preparación conjunta con Ramon Sastre.

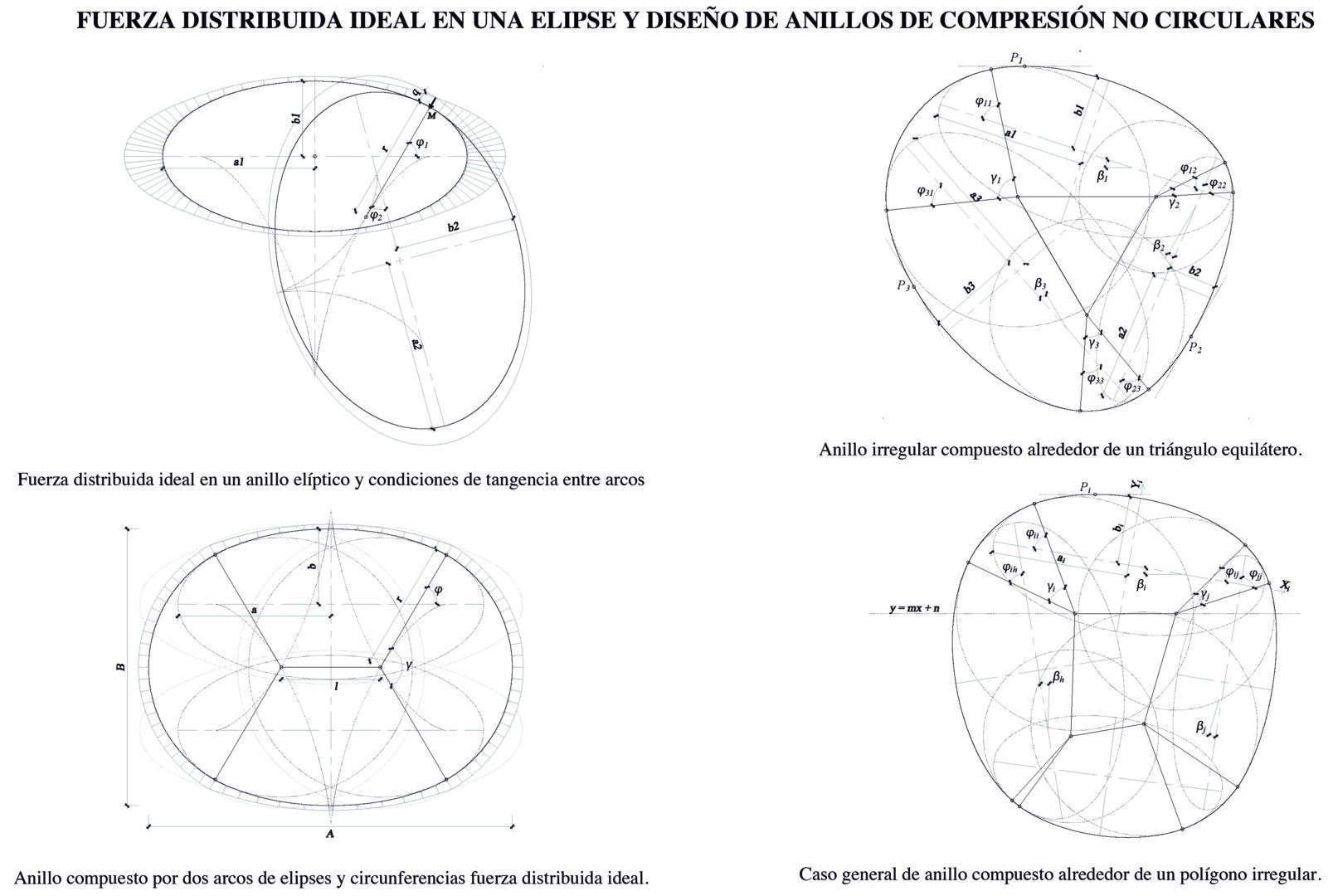
ORGANIZACIÓN:

La tesis está organizada en tres partes (planteamiento, desarrollo y conclusión) y dos anejos (bibliografía y modelos de cálculo). El desarrollo forma el cuerpo central de la investigación, donde se enuncian y resuelven los problemas planteados, empezando por los más elementales y aumentando el grado de complejidad progresivamente a medida que avanza el relato, de manera que sea coherente con el hilo argumental del proceso de investigación.

Todas las figuras y gráficos, a excepción de las que ilustran las referencias de proyectos, obras y patentes que aparecen en la primera parte, son originales de esta tesis.