Análisis histórico del comportamiento estructural de una viga sometida a flexión

ROBERT BRUFAU NIUBÓ

Doctor Arquitecto; Presidente de la Fundació Privada Institut d’Estudis Estructurals (IEE); ha sido Presidente de la Associació de Consultors d’Estructures (ACE) de 1987 a 1995; Profesor Titular del Departamento de Tecnología en la Arquitectura de la UPC, Ámbito de Estructuras; Profesor de postgrado sobre estructuras.
Socio Fundador de BOMA, SL; Socio Fundador de BBG estructures recerca i rehabilitacio SLP.
Galardonado con el Premio Internacional de Arquitectura Mies van de Rohe, con el Premio Nacional de Patrimonio Cultural. A lo largo de su carrera ha recibido 31 Premios FAD y ha sido finalista por más de 120 obras, siendo galardonado el 1996 con un galardón especial con un Premio Especial por su contribución al desarrollo de la arquitectura catalana durante los últimos 25 años.
Autor de diferentes obras técnicas y artículos técnicos.

La resolución del fenómeno del comportamiento resistente de cualquier sección de una viga sometida a flexión ha sido, a lo largo de la Historia de la Ciencia oficial, una de las mayores preocupaciones de los físicos, geómetras y matemáticos de todas las épocas. La evolución de las teorías sobre el comportamiento tensional de las secciones y, muy especialmente, sobre la posición de la «línea neutra» ha dado pie a numerosos estudios a lo largo de estos últimos años. El texto que sigue pretende recoger, de una manera bastante simplificada, los sucesivos pasos que se fueron dando al respecto. El tratamiento secuencial que se sigue en estas páginas próximas le permitirá al lector advertir los numerosos «errores» conceptuales que desde Galileo Galilei se cometieron —entre los siglos xvii y xix— hasta llegar al momento en que Navier y Barré de Saint-Venant asentaron de manera definitiva la teoría actual al respecto.

A manera de introducción, se reproduce, por su interés, parte del texto que el año 1996, el ingeniero de Caminos, Canales y Puertos, José Calavera Ruiz, publicó respecto a estos comportamientos, bajo el título «Breve Historia de la Fibra Neutra», publicado en la revista O.P. n.o 38, de Intemac:

Siempre me ha llamado la atención la larga cadena de curiosidades, titubeos, errores y aciertos que acompañan el descubrimiento del concepto y de la posición de la fibra neutra. Sorprendentemente es también larga la serie de científicos eminentes que estudiaron, con desigual fortuna, este tema.

Muchas veces se piensa que, históricamente hablando, la Física y sus derivaciones técnicas, como es el caso de la Resistencia de Materiales, han progresado cuando han estado disponibles las herramientas matemáticas necesarias. Es un grave error. Son las necesidades, teóricas y prácticas, que la Física va presentando, las que provocan el nacimiento de las teorías matemáticas necesarias para resolverlas.

Nuestro caso, el del concepto de la fibra neutra, ha sido una excepción. Como veremos, el primer paso lo dio Galileo el año 1638. Hasta esta fecha no hay constancia de que alguien hubiese estado interesado en el problema.

Lo anterior le puede sorprender a quien analice las realizaciones estructurales alcanzadas hasta este momento, especialmente si, como ocurre con frecuencia, el análisis es superficial. Es innegable que los maestros constructores de las Catedrales Góticas, por poner un ejemplo, llegaron a tener un importante dominio del tema. Pero no conviene exagerar, y por encima de todo, no conviene olvidar que lo que aprendieron lo adquirieron por procedimientos muy lentos y frecuentemente cruentos. Viollet-le-Duc lo expresa magistralmente cuando se refiere a ellos: «Buscando, encontraban. Iban siempre adelante, sin nunca decir Hemos llegado» (Viollet-le-Duc; «Dictionnaire raisonné de l’architecture française du xie au xvie siècle»).

Lo que, en cambio, no es aceptable es el argumento, que se escucha a veces, que tales maestros conocían a fondo el concepto del centramiento de las fuerzas, por el simple hecho de que las catedrales que hoy todavía podemos contemplar, las tienen centradas, especialmente en los arbotantes y en los contrafuertes. Lo único que, con rigor, se puede deducir de este hecho, es que las construcciones que tienen tal centramiento de fuerzas han llegado hasta nosotros, mientras que las que no (que eran muchas), se hundieron.

Esta es una manifestación más del falso concepto de la intuición estructural, ya que en lugar de concebir esta intuición como lo que es —un razonamiento a altísima velocidad, fruto de los estudios, experiencias y reflexiones previas— pretende presentarla como una alternativa al estudio. La ingeniería estructural no son solo fórmulas, pero no hay ingeniería estructural sin fórmulas.

NOTA: para la redacción de estas páginas que siguen se ha consultado principalmente, además del propio texto mencionado del Profesor J. Calavera, la Tesis Doctoral del arquitecto Juan L. Sánchez- Pro: «Alternativa histórica al proceso deductivo del conocimiento del cálculo de la Resistencia de Materiales » (ETSAB, 1974), y las fuentes que la guiaron, que
fueron, entre otras, «Histórique abregé» (Barré de Saint Venant), «A history of the theory of elasticity» (I. Toodhunter, K. Person) y «History of strenght of materials» (S. Timoshenko).

1. GALILEO GALILEI (1564 -1642)

Por sus ideas científicas opuestas a la ciencia escolástica, Galileo fue juzgado y condenado por herejía, siendo confinado en Arcetry el año 1633, donde comenzó a escribir un tratado sobre la Resistencia de los Materiales, bajo el título «Discorsi e dimostrazioni matematiche intorno a due nove scienze, atendendo alla mecanica e a i movimenti locali», que tuvo que publicar el año 1638 en Leyden (Holanda) por la prohibición que, después de su condena, había a la publicación de sus tratados en los países católicos.

En este texto introdujo el concepto de la resistencia a flexión de una viga, con el fin de poder relacionar las dimensiones de esta con la carga que podría resistir, y lo hizo basándose en la «ley de la palanca» de Arquímedes.

A partir de los dos célebres dibujos originales, que figuraban en las páginas 114 y 118, estableció las relaciones entre geometría y carga de rotura de la viga. Haciendo una cierta adaptación del texto original al lenguaje estructural moderno, lo enunciaba así:

«… Sea un prisma (viga) horizontal ABCD, empotrado en un muro para la cara AB, y con una carga E suspendida en el extremo CD. Es manifiesto que, si se ha de romper, lo hará por el punto B, donde se producirá el fulcro (pívot) de la palanca de brazo BC, mientras que el otro brazo de la palanca es el propio grueso del sólido (AB). En este segundo brazo se producirá la “resistencia”, que será la que se opondrá a que se separe la parte de sólido que está fuera del muro respecto a la que está dentro. Por lo dicho, el momento de la fuerza aplicada en C ha de ser igual al momento que produzca la resistencia que hay en AB, considerando como brazo relativo de esta palanca, no obstante, la mitad del grueso AB.»

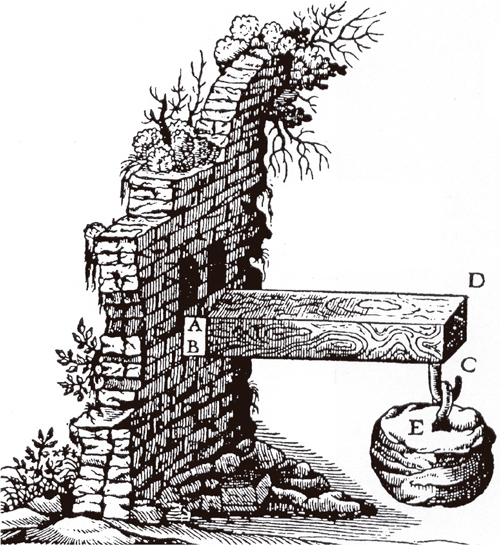
Galileo supuso, pues, que la rotura se produciría respecto a la fibra inferior de la sección (B), y que lo que la causaría sería una tensión uniforme (st ) actuando sobre toda la sección.

Para una sección rectangular (b 3 h), el momento resistente que sería capaz de aportar la sección (Mres) valdría, siguiendo el razonamiento de Galileo:

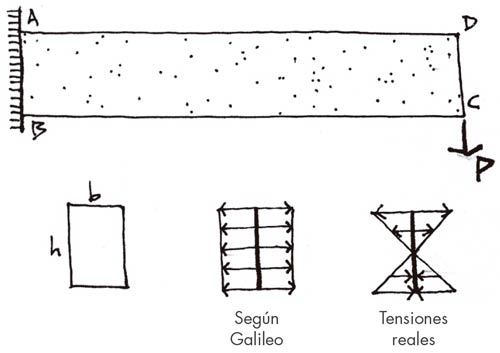
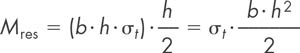
cuando actualmente no hay ninguna duda del que se obtendría en régimen estrictamente elástico, que sería:

Así, pues, las hipótesis de Galileo condujeron a un valor del momento resistente tres veces mayor que el que se obtendría en un análisis elástico riguroso.

Esta hipótesis errónea de Galileo fue empleada a lo largo de todo el siglo xviii por un buen número de ingenieros, arquitectos y constructores. Era una teoría peligrosa, ya que suponía que la barra tenía una resistencia mucho mayor que la que hoy día se consideraría en régimen elástico. Afortunadamente, sin embargo, los comportamientos plásticos han existido siempre, y, en este caso, habrían actuado de manera favorable, y bien se puede decir que muy probablemente ayudaron a evitar más de una catástrofe.

En la figura 4 se representan algunos esquemas más comprensibles para ayudar a entender estos comportamientos, el primero según las hipótesis de Galileo, el siguiente según un análisis elástico, y el tercero según un análisis con la sección totalmente plastificada, de donde se desprende que el momento que puede resistir la sección (Mres) de Galileo solo era el doble que el deducido en comportamiento plástico.

Tras su incorrecto planteamiento inicial y derivada de este, enunció una nueva propiedad que conducía a una peligrosa recomendación práctica, cuando en un discurso posterior, afirmó que «… una misma viga de diferente ancho que grueso, resistirá más a ser fracturada si se coloca vertical que plana… y lo hará en la proporción del ancho al grueso… ya que, en el primer caso la distancia de la resistencia, que es la mitad de la dimensión CA, será mayor que la distancia en el segundo caso, que solo será la mitad de BC…» y añadió, más tarde, «…conviene que la fuerza del peso T sea mayor que la fuerza del peso X, en la misma proporción que la mitad del canto de CA es mayor que la mitad del canto de BC…».

Esta afirmación, que era inicialmente correcta en lo que concierne a la proporción directa entre los módulos resistentes de cada una de las secciones y su canto, se convertía en una recomendación muy peligrosa cuando, como conclusión, mantenía la misma proporción entre el canto de las vigas y la carga que cada una de ellas podía soportar.

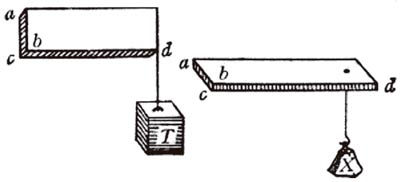
Galileo no advirtió que la relación entre los momentos de inercia de las dos secciones no era linealmente proporcional a la relación entre sus cantos, sino que estaba elevada al cuadrado. Al ser la relación entre las flechas inversamente proporcional a los respectivos momentos de inercia, la conclusión de Galileo causaría deformaciones inaceptables para quienes dispusieran la sección apaisada. Analizando, como ejemplo, dos vigas (V₁ y V₂), con secciones de 10 x 30 cm y 30 x 10 cm respectivamente, resultarían las siguientes proporciones:

• Proporción entre los módulos resistentes:

• Proporción entre los momentos de inercia:

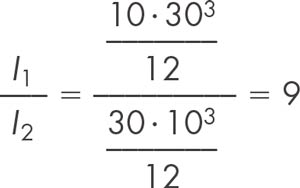
2. ROBERT HOOKE (1635-1703)

Aún considerando que no se ocupó directamente de las vigas ni, por tanto, de la línea neutra, Hooke proporcionó un avance importante con su publicación «De potentia restitutiva or of springs explaining the power of springings bodies», en las «Philosophical transactions» de la Royal Society. En este trabajo, Hooke estableció el principio «Ut tensio, sic vis» («Tal es el alargamiento, así es la fuerza»). Las teorías de Hooke allanaron el camino a muchos de los que vinieron después.

Galileo trabajó sus teorías a lo largo del período 1633-1638, y lo hizo considerando como único modelo físico el sólido rígido, y, probablemente, sus resultados no fueron suficientemente satisfactorios al no tener en consideración la deformabilidad de los cuerpos.

Tuvieron que pasar unos cuantos años hasta que Robert Hooke, a lo largo del período 1660-1678 elaborase su teoría elástica de los resortes en el texto «Potentia Restitutiva or spring» (1678). En esta publicación es donde Hooke enunció su célebre principio «Ut tensio, sic vis». Evidentemente, cuando Hooke hablaba de «springs» se estaba refiriendo tanto a muelles espirales como a cualquier cuerpo o barra elásticos, y en su célebre dibujo así lo dejó claro al representarlo de ambas maneras.

Realizó gráficamente tres experimentos, uno con un helicoide plano vertical, del que colgó un plato de carga, el segundo con un muelle espiral y el tercero con una simple barra metálica vertical. Al cargarlos de este modo registró los alargamientos sufridos y dedujo que siempre existía proporcionalidad total entre los alargamientos medidos y los pesos que se habían colocado en cada caso (fig. 7).

En lo concerniente a la flexión, Hooke extrapoló los resultados anteriores a una viga en voladizo, diciendo: «Igual se puede concluir si el ensayo se realiza con una pieza de madera seca que flechará si un extremo permanece en posición horizontal y del otro se suspenden pesas, que lo hacen descender al flectar… y recuperará su posición primitiva al descargarse».

Hooke no empleó en ningún momento el concepto de «tensión», y mucho menos el concepto de «resistencia» de Galileo, ya que se limitó a poner en relación los alargamientos con las cargas que los ocasionaban, sin embargo sí que hizo una acertada aproximación al comportamiento a flexión, distinguiendo entre fibras traccionadas y fibras comprimidas, tal como queda patente en el dibujo que se acompaña, que, con una traducción adaptada, viene a decir:

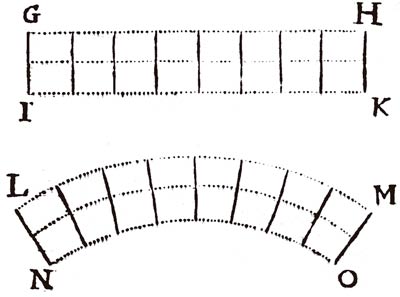
«Habiendo explicado el más simple de los comportamientos a tracción de los cuerpos sólidos, será fácil explicar el comportamiento elástico de un cuerpo a flexión, suponiendo que dos de sus fibras GH y KI, al ser solicitadas por una fuerza externa, flechan, convirtiéndose en LM y NO. La fibra LM se estirará mientras que la fibra NO se acortará, y lo harán en proporción a la flexión, y, en consecuencia, las mismas proporciones y leyes se deberán cumplir para volver a su estado primitivo».

3. EDME MARIOTTE (1620-1684)

El monje Mariotte tuvo el privilegio de ser el primer científico capaz de juntar los conocimientos separados de Galileo y de Hooke. Utilizó el modelo clásico de la viga en voladizo del primero como motivo de experimentación, pero su visión contemplaba ya una cierta intuición del comportamiento elástico de los materiales, a la manera del segundo.

Centrando estas líneas en lo concerniente al análisis a flexión de las vigas, debe decirse que Mariotte se basó, al igual que Galileo, en el principio de la palanca de Arquímedes. En una primera etapa supuso la rotura de la sección AD girando respecto al fulcro, situado en el punto D, el más bajo de la sección, pero aceptó de inmediato que no todos los puntos trabajarían con la misma tensión, sino con una distribución triangular. Lo expresó mediante la siguiente teoría:

«…Si la fibra A por romperse ha de ser estirada 16 pequeñas partes, es evidente que las fibras G, I y H no necesitarán toda su resistencia para impedir la rotura de la fibra A, sino que ellas resistirán en proporción a su distancia al punto D…»

Con este razonamiento, además de aceptarse una distribución triangular de las tensiones, se aceptaría también una distribución triangular de los alargamientos.

Mariotte interpretó que todas las fibras longitudinales de la sección se estiraban, y que si se cumplía hasta la rotura la proporcionalidad entre los alargamientos y las cargas, la distribución de las resistencias (tensiones) sería triangular y daría una resultante que valdría justamente la mitad de la resistencia absoluta que obtuvo Galileo.

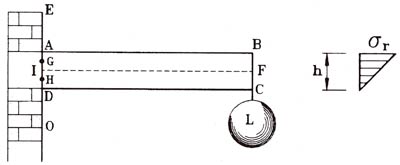
El momento resistente de la sección sería, según Mariotte:

que todavía daría un valor doble que el que se deduciría de un comportamiento elástico puro, aún considerando que hizo una reducción de un 50 % respecto al valor que obtuvo Galileo.

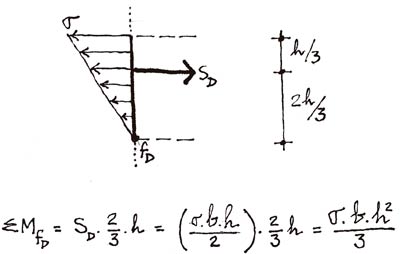
Pero Mariotte realizó, hacia el final de su vida, unos ensayos reales para comprobar sus conclusiones teóricas anteriores. Los resultados no le satisficieron, y Mariotte se vió obligado a rectificar sus planteamientos tensionales. Después de observar el comportamiento de determinados materiales sometidos a flexión, dedujo la aparición, en una misma sección, de deformaciones de tracción y de compresión. Lo dejó escrito en las siguientes líneas:

«…la experiencia nos enseña que un pequeño bastón que deformamos para romperlo, contrayéndose por el lado cóncavo de su curvatura, ha de estirarse necesariamente por su lado convexo, deduciéndose, de este hecho, que es necesario que haya un esfuerzo para comprimir la zona cóncava…».

Concluyó este razonamiento con el esquema de la figura 12, diciendo:

«…Si ABCD es una barra cuadrada empotrada en un muro, se puede entender que desde D  hasta I, que es la mitad del grueso DA, los puntos sufren compresiones, aún considerando que en mayor medida los próximos a D que los próximos a I, y que desde I hasta A se estiran, con el mismo criterio…»

Probablemente su muerte hizo que quedase inacabada su teoría, que el año 1686 fue publicada póstumamentepor su discípulo Philippe de la Hire, dentro del libro «Traité des mouvements des eaux». En cualquier caso, los avances introducidos por Mariotte fueron de una gran importancia.

4. JACQUES BERNOUILLI (1654-1705)

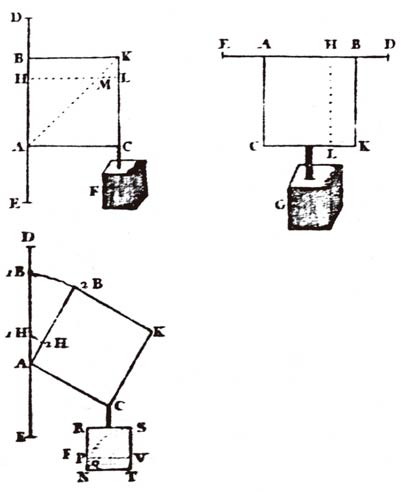
Bernouilli fue, el año 1694, el primero que estableció la ecuación de la elástica (o deformada) de una viga flectada. Para hacerlo se basó en los cuatro «lemas» que se resumen así:

Lema 1. «Las fibras de un mismo material y con el mismo grueso, traccionadas o comprimidas por la misma fuerza, se alargarán o se acortarán proporcionalmente a sus longitudes».

Lema 2. «Las fibras de material homogéneo y de la misma longitud, pero de distinto grueso, se alargarán o se acortarán con la misma intensidad si las fuerzas que las solicitan son proporcionales a sus espesores».

Lema 3. «Las fibras de material homogéneo, con la misma longitud y el mismo grueso, pero solicitadas por cargas distintas, no se alargarán o se acortarán proporcionalmente a estas cargas; así, el alargamiento o el acortamiento producidos para la carga mayor es al alargamiento o el acortamiento producidos para la carga menor, en menor proporción que lo son aquella carga y esta». Este lema permite intuir un cierto planteamiento «plástico» del comportamiento del material, novedad que el propio Bernouilli volvió a tratar a lo largo de los años siguientes.

Lema 4. «La misma fuerza que hace flectar una barra ABCD de AB hasta GF, traccionando una parte de sus fibras en la cantidad correspondiente al triángulo BSF, y comprimiendo la otra parte en el triángulo ASG, será capaz, teniendo el fulcro en A, de traccionar el conjunto de todas las fibras la magnitud del triángulo ABF».

Aunque en este cuarto Lema intuyó la presencia de una parte inicialmente comprimida de la barra —la correspondiente al tramo AS—, posteriormente volvió, de manera incorrecta, a situar la posición final del fulcro en el punto A, aceptando que toda la sección estaría traccionada. Este error lo corrigió a lo largo de exposiciones futuras, como la definitiva del año 1705, en la que ya aceptó que toda la sección de la viga flectada estaría colaborando en la resistencia, pero con la mitad de las fibras traccionadas y la otra mitad comprimidas. Esto le permitió resolver la ecuación de la elástica en la forma actualmente aceptada.

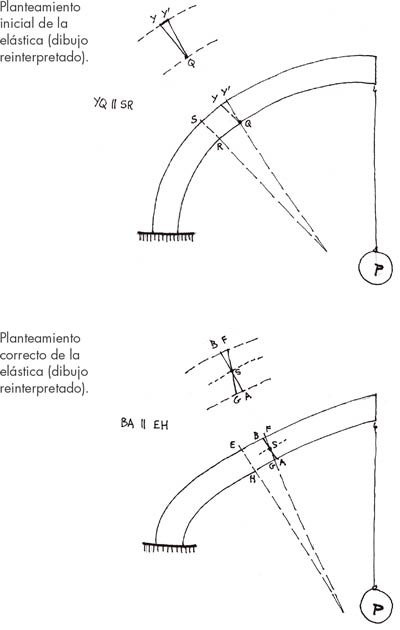
5. GOTTFRIED WILHEMOS LEIBNITZ (1646-1716)

No deja de ser curioso que una personalidad tan notable dentro del mundo científico de aquellos momentos, como era Leibnitz, manifestase su interpretación de las teorías de Galileo y de Mariotte, y que lo hiciese erróneamente. A su publicación «Demostratione novae de resistentia Solidorum» (1684) cita los trabajos de Mariotte, pero continua considerando que el fulcro de la palanca sigue estando en el punto inferior de la sección (A).

La figura 17 no deja ninguna duda sobre su visión del problema, que se podría resumir en estos tres puntos:

• a) Antes de ocurrir la rotura de una viga en voladizo, se producirá su flexión.
• b) Se cumple la ley de proporcionalidad elástica entre alargamientos y resistencias.
• c) La situación del fulcro de la palanca ficticia se produce en la base de la sección, tal y como lo plantearon Galileo y Mariotte en su primera hipótesis.

Este conjunto de consideraciones sobre la posición de la línea neutra es conocido como la «hipótesis de Mariotte-Leibnitz», que, sorprendentemente, todavía se consideraba válida en tratados suficientemente prestigiosos como el de Pierre S. Girard («Traité analytique de la resistence des solides», 1798), el de Peter Barlow («An essay on the strenght and stress of timber», 1817) y el de A. Duleau («Essai theórique et experimental sur la résistance du fer forgé», 1820).

6. ANTOINE PARENT (1666-1716)

Entre 1704 y 1713, Parent se interesó en el tema de la resistencia de los sólidos, publicando algunos textos sobre la flexión de las vigas, llegando a encontrar en los últimos años (1713) soluciones muy correctas respecto al comportamiento tensional de las secciones para el caso de la flexión pura. Él fue el primero que estableció, dentro del texto «Recherches de mathématiques et de physique» la forma correcta de trabajar de la sección, diciendo que «…en una viga flectada, el sumatorio de las resistencias de las fibras comprimidas había de ser exactamente igual al sumatorio de las resistencias de las fibras traccionadas…», facilitando con este criterio la base analítica para deducir en cada caso la posición de la línea neutra.

Comparando la distribución triangular de Mariotte (y de Leibnitz) —con fulcro en el punto inferior— que figura en el primer esquema, con la que propone Parent —con fulcro en el punto central— que figura en el segundo, le resulta a Parent que la sección puede aportar un momento resistente con valor mitad que lo que le resulta a Mariotte. El valor que se obtendría con la distribución de Parent coincide con el momento resistente que se deduciría de un comportamiento elástico perfecto.

Desgraciadamente, quizá por tratarse de un hombre impopular, formado académicamente en el mundo de las leyes y que se manifestó siempre muy crítico con los investigadores de su tiempo, o quizá por no estar dentro de los circuitos científicos «a la moda», lo cierto es que las propuestas de Parent no tuvieron ninguna repercusión, y el mundo científico de la época las ignoró, hasta que, sesenta años más tarde, Coulomb y Navier las reinventaron, ya a finales del siglo XVIII.

7. CHARLES AUGUSTIN COULOMB (1736-1806)

Coulomb fue el autor de un texto fundamental para llegar a la madurez de la ciencia de la Resistencia de los Materiales, al presentar en la Academia de Ciencias francesa la memoria «Essai sur une application des regles de maximis et minimis a quelques problemes d’estatique relatifs a l’architecture» (1777). Fue también uno de los primeros teóricos que realizó ensayos empleando modelos reales de rotura para conocer la capacidad resistente de las barras.

En este tratado, Coulomb introdujo un concepto nuevo: la «fuerza de cohesión», entendida como el cociente entre la «resistencia absoluta de la sección» (o fuerza total que podía resistir esta  sección) dividida por su superficie. Si la resistencia absoluta equivale al valor de la fuerza resultante que actuaría sobre la sección en el momento de romperla, la fuerza de cohesión identificaría el valor de la «tensión normal de rotura» (s) del material de la sección.

Para analizar vigas sometidas a flexión como consecuencia de la aplicación de cargas verticales externas, Coulomb recurrió a la aplicación de las ecuaciones generales de equilibrio de la estática, deduciendo así que, en cada sección vertical, deberían haber también «fuerzas de cohesión verticales», el sumatorio de las cuales debería ser equivalente a la carga vertical aplicada.

Así apareció, por primera vez, el concepto del esfuerzo cortante y la «tensión vertical» (t) ligada a este esfuerzo, y en dirección tangente en la sección.

Coulomb hizo todavía otro paso adelante al sugerir que las tensiones verticales y las horizontales deberían analizarse conjuntamente, apareciendo, de manera implícita, las «tensiones  combinadas», que podrían ser causantes de roturas en planos no coincidentes con el plano vertical o con el horizontal. Valga, como ejemplo, la conclusión a la que llegó respecto a la rotura a 45° que sufriría un prisma vertical sometido únicamente a la acción de cargas compresivas axiles.

En lo que concierne a la posición de la línea neutra, Coulomb llegó a las mismas conclusiones a las que, 60 años antes, había llegado Antoine Parent. Parece ser que Coulomb desconocía los escritos de Parent, pero los criterios para posicionar la fibra neutra y para interpretar la distribución de las tensiones normales en la sección fueron totalmente coincidentes.

Muchos años antes, Jacques Bernouilli (ver su Lema 3.o) reconocía como posible un reparto tensional no elástico, Coulomb abrió también sus teorías a la posibilidad de que se pudiesen producir asimismo distribuciones no lineales de las tensiones perpendiculares en la sección, pero lo limitó a los materiales que no siguiesen las leyes del comportamiento elástico.

Se podría decir, sin riesgo de equivocación, que Coulomb fue el padre del actual análisis tensional, siendo de una gran importancia su influencia en las generaciones de ingenieros del siglo xix, aún considerando que sus teorías tuvieron una difusión muy lenta entre los sabios de la época. Su obra científica no se limitó al análisis tensional, sino que abarcó también numerosos trabajos sobre muchos otros aspectos de la construcción arquitectónica o ingenieril. Encontramos, por ejemplo, su nombre asociado al cálculo de los empujes del terreno y de los muros de contención así como al estudio del trazado de los arcos y de las bóvedas.

8. LOUIS-MARIE HENRY NAVIER (1785-1836)

Ya en el año 1819 consideraba que debería darse la igualdad de los momentos producidos por las tensiones de tracción y las de compresión, como condición principal para fijar la posición de la línea neutra, lo que solo era válido, no obstante, para el caso de secciones simétricas sometidas a flexión simple.

En un nuevo paso adelante llegó a la conclusión de que, para una posición dada de la línea neutra, la ecuación de equilibrio de los momentos de las fuerzas externas y de las resistencias le permitiría dar la expresión exacta de la resistencia a flexión de una sección, aproximándose, así, a los planteamientos de Coulomb, siendo, a partir de este momento, cuando Navier, el año 1826, llegó a la solución exacta del problema, que explicó en el texto «Resumé des lessons données a l’Ecole des ponts et chausées sur l’application de la Mécanique a l’établisement des constructions et des machines».

Definió la flexión como un esfuerzo que actúa en sentido perpendicular a la longitud del sólido, que se deforma curvándose, comprimiendo y acortando sus fibras cóncavas y traccionando y alargando las convexas, mientras que otras fibras, situadas en el interior, permanecen invariables.

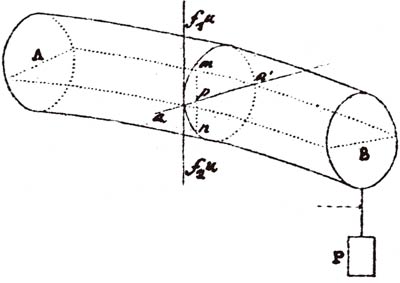
Al analizar la figura 24 fijó las siguientes condiciones básicas de equilibrio estático:

• a) Las fuerzas verticales han de estar en equilibrio: «Los alargamientos y los acortamientos de las fibras longitudinales han de producir, en la sección, la aparición de fuerzas verticales, la suma de las cuales ha de igualar el peso aplicado P».
• b) Las fuerzas horizontales han de estar en equilibrio: «El sumatorio de las fuerzas horizontales, producidas por los acortamientos y por los alargamientos, ha de ser nula».
• c) Los momentos han de estar en equilibrio: «La suma de los momentos respecto al eje aa9, de las fuerzas verticales y horizontales que actúan en la sección y del peso aplicado P, ha de ser nula».

Fue la resolución de estas tres ecuaciones de equilibrio lo que le permitió a Navier establecer la ecuación de la línea neutra, que, en el caso de flexión pura y simple, debería pasar invariablemente por el centro de gravedad (c.d.g.) de la sección. El lector encontrará en este y en el siguiente tema de este artículo la aplicación actual de esta teoría, con expresiones más modernas y de operatividad más fácil.

Como conclusión de sus avances, Navier enunció su célebre hipótesis: «Los alargamientos o acortamientos (y, en consecuencia, las tensiones normales) de cada fibra de una sección serán  directamente proporcionales a las distancias que habrá desde el punto correspondiente de la fibra en cuestión hasta la línea neutra de la sección que se analiza».

9. THOMAS TREDGOLD (1788-1829)

Tredgold no se caracterizó por hacer ningún avance significativo en este tema, pero en su texto «The elementary principles of charpentry» (1820) aparece, por primera vez, la actual denominación de la «línea neutra», para definir la recta que separa la zona traccionada de la zona comprimida en cada sección. Lo hizo bautizándola en inglés como «neutral axis».

10. LEONARDO DA VINCI (1452-1519)

Es bueno acabar este apasionante tema por lo que debería haber sido su comienzo. En la mayoría de tratados sobre Resistencia de Materiales se suele considerar a Galileo Galilei (1564 – 1642), a Edme Mariotte (1620-1684) y a Jacques Bernouilli (1654 – 1705) como los pioneros de la teoría moderna sobre el comportamiento de los cuerpos sometidos a flexión.

Resulta, no obstante, sorprendente que Leonardo da Vinci hubiese expuesto, más de cien años antes, el fenómeno de la flexión de una barra cargada, y que lo hiciese con una precisión tan sorprendente, avanzando perfectamente la posición de la línea neutra, la distribución de las deformaciones de las fibras de la sección, e incluso, el propio Principio de Poisson sobre la deformación transversal… y todo esto en un solo dibujo! (fig. 27).

¿Por qué, pues, el desaprovechamiento posterior de las experiencias de Leonardo por parte de los físicos, matemáticos, arquitectos y constructores, hasta el punto de que tuviese que ser  redescubierta muchos años más tarde, después de haberla madurado científicos tales como Galileo, Hooke, Mariotte, Leibnitz, Coulomb y tantos otros?

La explicación podría buscarse en diversas causas:

a) Los manuscritos de Leonardo sufrieron una gran dispersión, perdiéndose varios trabajos y quedando muchos otros olvidados en archivos de bibliotecas o castillos, sin prácticamente salir a la luz durante siglos.

b) Los historiadores de los siglos xvi y xvii, mayoritariamente filósofos y profesores de ciencias o de literatura, no prestaron mayor atención a los trabajos teóricos sobre mecánica, hasta el punto que un ciudadano remarcable como Joseph Louis de la Grange (1736 -1813) escribiese el año 1788: «…el intervalo que separa a Arquímedes de Galileo desaparece en la Historia de la Mecánica…».

c) Con respecto a sus contemporáneos, la excesiva fe de Leonardo en la experimentación lo llevó a enfrentarse abiertamente a autores de renombre de su época, haciéndolo sin el bagaje matemático de estos, tal como reconocía al decir: «…muchos pensarán, con razón, poder censurarme argumentando que mis demostraciones van en contra de la autoridad de algunos hombres de gran prestigio, pero estos tienen un juicio equivocado sobre ellas y no aceptan el hecho de que mis razonamientos hayan nacido de la simple experiencia, la cual es la auténtica maestra…».

d) Finalmente, su propia manera de trabajar no favorecía, precisamente, la propagación de sus trabajos, ya que si bien planteaba los enunciados de sus Teoremas, raramente los acompañaba de cálculos justificativos o de referencia a experiencias concretas, habiendo formulado, e, incluso, numerado, un índice de un tratado que agrupase todos los cálculos de sus Teoremas, trabajo que se ha perdido, y que —probablemente, si atendemos a la opinión de algunos historiadores— nunca fue escrito. Su inconstancia en este aspecto de su trabajo queda puesto de manifiesto por el historiador C. Truesdell, en sus «Ensayos de historia de la Mecánica», donde afirmaba que:

«… Raramente Leonardo escribió más de un solo párrafo sobre cualquier materia…»

añadiendo, a continuación:

«… La curiosidad de Leonardo no conocía límites. Observaba y dibujaba como nadie, pero la virtud del orden no le fue dada, y, por tanto, era incapaz de crear una teoría. Como botón de muestra basta con sus cuadernos de apuntes, a los que nunca llegó a dar una forma definitiva…».

y, en un tono mucho más crítico:

«… La ciencia humana nunca ha sido un montón de observaciones y conjeturas, ni únicamente siendo verosímiles las observaciones y buenas las conjeturas. Por esta razón se podrían rechazar nueve décimas partes, o más, de todo lo que escribió Leonardo, por no haber contribuido en absoluto al desarrollo de la ciencia. Lo que un hombre aporta a la posteridad no es la suma algebraica de sus esfuerzos, sino lo mejor de entre ellos. Por tanto, deberíamos buscar entre un montón de escoria para encontrar los tesoros que en él pueden esconderse…».

para concluir:

«… Al pasar de las leyes numéricas a la representación gráfica es cuando Leonardo da Vinci adquiere su verdadera dimensión…».

Es apasionante, por su valor histórico y por la singularidad de su contenido, la lectura de la página de dibujos en la que Leonardo da Vinci intentó explicar el comportamiento a flexión de las vigas. Se recomienda al lector que se entretenga unos minutos intentando interpretar lo que quería transmitir su autor.