Diseño de estructuras metálicas basado en el análisis global del pandeo

DR. JÓZSEF SZALAI
Doctor Ingeniero Civil por la Universidad de Tecnología y Economía de Budapest BUTE; profesor asociado en la facultad de ingeniería civil de la universidad de SzentIstván de Hungría; director Técnico de ConsteelSolutionLtd; jefe de desarrollo de I+D de la empresa KÉSZ Ltd y miembro del comité técnico TC8 (Estabilidad) de la ECCS.

DR. FERENC PAPP
Doctor Ingeniero Estructural por la Universidad de Tecnología y Economía de Budapest BUTE; Director de departamento en la Universidad de SzéchenyiIstván de Budapest; y Miembro del comité técnico TC8 (Estabilidad) de la ECCS.

ALBERT JIMÉNEZ MORALES
Ingeniero Industrial titulado en la Universidad Politécnica de Catalunya UPC; Profesor asociado en el departamento de Ingeniería de la construcción de la escuela de Ingenieros de Caminos, Canales y Puertos de Barcelona; y Director técnico de I+D de la empresa Construsoft SL

Cada día es más habitual la realización de modelos 3D completos con gran detalle para realizar cálculos estructurales y verificaciones según distintas normativas, sin embargo, en la manera tradicional de tratar estos modelos, sólo se acaba utilizando el 3D para el cálculo de esfuerzos en todas las barras y no se aprovecha todo el potencial de la definición geométrica del modelo para el diseño de la estabilidad de los elementos estructurales. Esto suele ser debido a la complicación para los programas tradicionales de estructuras en realizar cálculos de los modos de pandeo global “incluyendo la torsión” en los modelos tridimensionales donde éstos cálculos pueden reflejar la influencia que tienen algunos detalles constructivos definidos en el modelo analítico en la estabilidad de elementos, como es el caso de las excentricidades existentes entre uniones de barras, excentricidades en apoyos, posición exacta de las cargas y arriostramientos etc. Es por este motivo, que los parámetros relacionados con la verificación de pandeo de elementos, como son los coeficientes β para el pandeo por flexión, o parámetros C para la verificación del pandeo lateral, se acaban calculando mediante tablas, libros o usando programas de cálculo especiales, para introducir estos parámetros, como información adicional, en los elementos estructurales del modelo 3D original para que puedan realizar verificaciones correctas a estabilidad.

Este artículo pretende mostrar cómo es posible utilizar herramientas informáticas de fácil manejo para obtener resultados de los modos de pandeo global en modelos 3D estructurales y realizar un diseño práctico basado en el método general definido en el punto 6.3.4 de la EN 1993-1-1 y que permite verificar, de manera directa, las estructuras a partir de los resultados de sus modos de pandeo por flexión, flexión-torsión y pandeo lateral y que es aplicable a perfiles armados de inercia variable y perfiles reforzados.

1. Análisis global de pandeo incluyendo la torsión y el alabeo de las secciones.

Este capítulo trata de explicar la utilidad de utilizar elementos finitos lineales usando 7 grados de libertad por nodo, donde el alabeo de la sección se incluye en el problema matemático. Esto permitirá a los ingenieros entender, de una manera más precisa, el comportamiento estructural real y utilizar los resultados del análisis del pandeo global y segundo orden para el diseño práctico de estructuras (explicado en el siguiente punto).

1.1 Formulación básica utilizando elementos finitos especiales de 7 G.D.L.

En esta sección se presenta de manera resumida las bases teóricas del elemento finito viga-columna para paredes delgadas de 7 grados de libertad (7 GDL) por nodo. Las bases teóricas de este elemento fueron originalmente definidas por Borsoum and Gallagher (1970)[1]. La definición del elemento finito utilizada en programas de diseño estructural prácticos como ConSteel fue publicada por Rajasekaran en el famoso libro de texto de Chen y Atsuta (1977)[2]. Elementos finitos similares se publicaron por Kindmann and Kraus (2007) [3]. Este elemento finito fue modificado por Turkalj et al. (2003)[4] para poder considerar problemas con grandes desplazamientos. El software ConSteel utiliza el elemento finito de 7GDL original definido por Rajasekaran y está especialmente desarrollado para su utilización en elementos de secciones abiertas donde el alabeo tiene un efecto muy importante en el comportamiento de la sección transversal, y este efecto se puede considerar mediante la utilización de 7 GDL como muestra la Fig. 1.

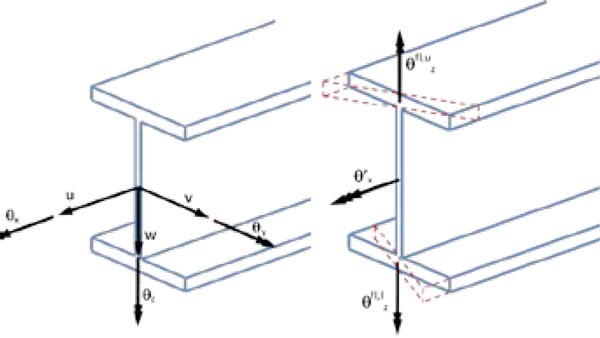
Los primeros 6 GDL son los desplazamientos convencionales (u, v, w) y rotaciones (θ_x, θ_y, θ_z) de acuerdo al sistema de coordenadas local del elemento, y el séptimo GDL es matemáticamente la primera derivada del giro torsional alrededor del eje longitudinal (θ_x’); matemáticamente éste representa el alabeo de la sección el cual es una consecuencia directa de la torsión en secciones abiertas de paredes delgadas. La Fig. 1 muestra el efecto del alabeo de la sección en un perfil tipo I, cuando las alas sobresalen del plano original de la sección. En este caso el GDL del alabeo se puede considerar como una rotación de las alas dual y opuesta alrededor del eje perpendicular a su anchura (en este caso el eje local “z”). Esto nos permite considerar los 7 componentes de desplazamientos y fuerzas nodales en los dos nodos del elemento (‘j’ and ‘k’) de la siguiente manera:

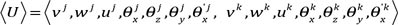
Usando estos vectores se puede establecer el equilibrio del elemento como:

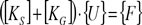
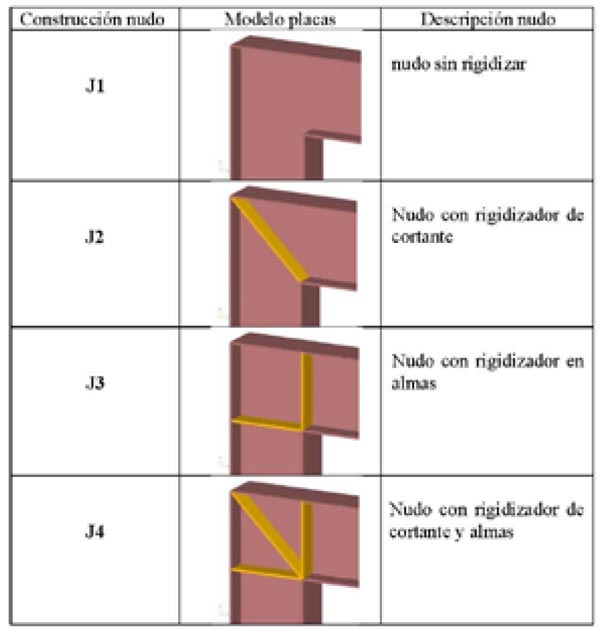
Donde [K_S] es la matriz de rigidez elástica (primer orden), [K_G] es la matriz de rigidez geométrica (segundo orden) y estas matrices de rigidez de 14×14 se pueden escribir como se muestra en la Tabla 1 y la Tabla 2, donde se remarcan los términos adicionales o que son diferentes, comparando con las matrices de rigidez convencionales de 12×12. Se puede apreciar que los elementos de la matriz de rigidez [K_S] se expresan en términos de parámetros geométricos, sin embargo, los elementos de la matriz de rigidez [K_G] se expresan en términos de resultantes de tensiones tales como P, f_y, f_z, m_y^j, m_z^j y K. Este último se denomina coeficiente de Wagner, y depende de la distribución de las tensiones normales σ_x en el elemento.

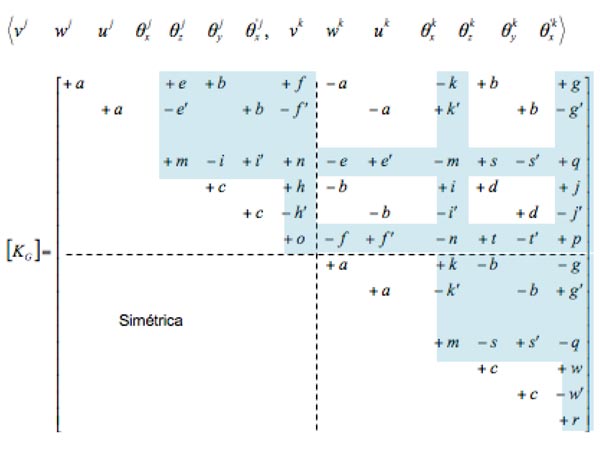
(el símbolo ’ indica que z_ω, m_y and f_z debería substituirse por y_ω, m_z y f_y)

El significado de las denotaciones pueden encontrarse en Chen and Atsuta (1977)[2]. La cantidad de términos adicionales, especialmente en la matriz de rigidez de segundo orden, demuestra la diferencia substancial entre considerar la mecánica convencional con elementos de 6 GDL o de 7 GDL. Estos términos hacen posible resolver problemas complejos en segundo orden incluyendo la torsión con alabeo, y realizar análisis globales de pandeo considerando todos los modos posibles (pandeo por flexión, torsión, flexión-torsión, pandeo lateral y cualquier interacción entre ellos).

1.2 Análisis de esfuerzos y deformaciones en segundo orden

En este apartado se analiza cómo se resuelve el modelo teórico del elemento estructural recto y uniforme de acero de la Fig. 2.

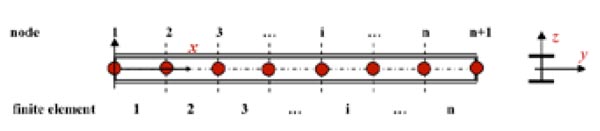
El elemento puede determinarse como un sencillo conjunto de n números de elementos finitos y n+1nodos. La ecuación de equilibrio del elemento se puede escribir usando la Eq. (3) juntamente con las matrices de rigidez del elemento dadas en la Tabla 1 y la Tabla 2:

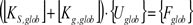
o en su forma reducida,

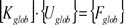
Considerando la Eq. (3) el vector desplazamiento y la matriz de rigidez global se puede expresar de la siguiente manera:

Todas las filas relacionadas con el séptimo grado de libertad en la ecuación de equilibrio Eq. (5) son una confirmación del equilibrio de los dos bimomentos tomados en los extremos de los dos elementos conectados en el nodo (Fig. 3):

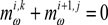
Debido a que el bimomento se debe expresar como la segunda derivada del giro de la sección, y que esta última se aproxima por un polinomio de tercer grado, la Eq. (7) asegura también la compatibilidad del alabeo. En cualquier otro caso (e.j. sección variable; elemento no recto; nudos 3D donde los elementos tienen diferentes direcciones, y así sucesivamente) la Eq. (7) no es estrictamente correcta. Sin embargo, a falta de una solución analítica precisa, la Eq. (7) puede aplicar de forma general.

1.2.1 Ejemplo de cálculo de una viga simplemente apoyada contorsión

Este ejemplo demuestra la diferencia entre los resultados del elemento convencional de 6 GDL y el elemento de 7 GDL presentado utilizando la teoría de primer y segundo orden. La Fig. 4 muestra el caso de una viga simplemente apoyada con una carga concentrada en el centro del vano con una pequeña excentricidad lateral definida de 40mm. (El software ConSteel permite definir en las cargas un valor de excentricidad para facilitar al usuario la consideración de este efecto evitando la introducción de elementos auxiliares o momentos para simular el torsor equivalente que produce la carga excéntrica).

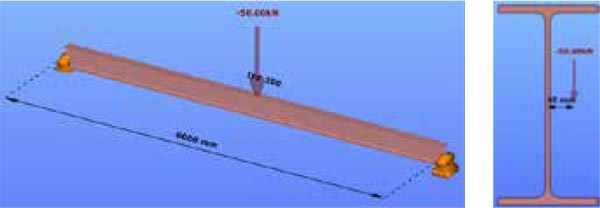
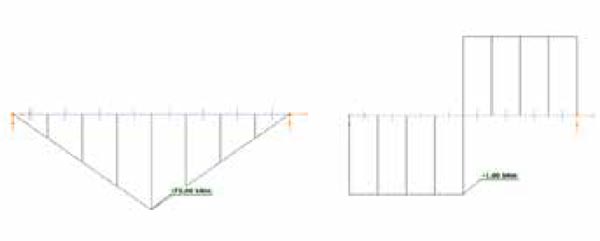
Utilizando el elemento de 6 GDL no se obtienen diferencias entre el análisis de primer y segundo orden y los resultados obtenidos del análisis son únicamente un momento flector respecto el eje fuerte My de 75 kNm y un momento torsor de 1 kNm mostrados en la Fig. 5.

Mediante la utilización del elemento de 7GD es posible obtener resultados más aproximados del comportamiento real de la pieza en estas condiciones, como es el caso de la torsión restringida de alabeo (obtención de un bimomento) y considerar los efectos de segundo orden en el giro de la sección, dando lugar a la aparición de un momento flector respecto al eje débil del perfil Mz, debido al efecto que tiene la carga vertical al girar las sección produciendo una flexión adicional respecto a ese plano.

En la Fig. 6 se muestran todos los resultados obtenidos mediante el análisis de segundo orden con el elemento de 7GDL.

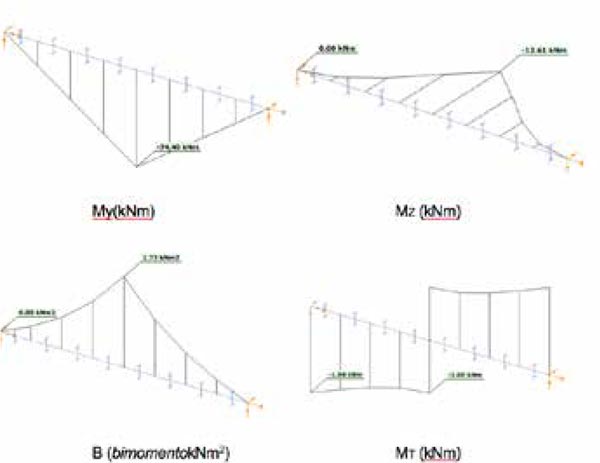
Estos resultados más próximos del comportamiento de un perfil sometido a torsión, ponen de manifiesto la gran influencia que tiene ésta en el resultado final de tensiones y deformaciones como puede verse en la Fig. 7 y 8, ya que a las tensiones normales debidas a la flexión en el plano y fuera del plano se suman a las tensiones normales debidas a la torsión no uniforme de alabeo (bimomento).

En la Tabla 3 se muestran los resultados de esfuerzos calculados en el centro del vano en primer y segundo orden (flexión respecto eje fuerte, flexión respecto eje débil, bimomento y tensiones normales máximas) usando elementos de 6GDL y de 7GDL, donde se pueden extraer las siguientes conclusiones interesantes:

• El elemento de 6 GDL calcula únicamente la torsión simple o constante de St. Venant, y consecuentemente no ofrece resultados para el bimomento, a pesar de que éste tiene un efecto muy significante en las tensiones normales.
• En el cálculo con el elemento de 6 GDL no existe diferencia alguna entre el análisis de primer y segundo orden, sin embargo, debido la flexión en el plano y al giro de la sección aparecen efectos importantes de segundo orden que generan flexión fuera del plano.
• Finalmente se demuestran tensiones más realistas en la sección muy superiores (más de 3 veces) comparado con el cálculo clásico con 6GDL, debido al cálculo más preciso donde se consideran los efectos de segundo orden en el bimomento y el efecto de la flexión fuera del plano debido a la rotación del perfil.

1.3 Análisis lineal del pandeo en barras

La condición general para los problemas de pandeo (como el pandeo por flexión “Flexural Buckling” FB); pandeo lateral “lateral-torsional buckling” LTB; o pandeo combinado “coupled buckling” CB) es que la carga no incluya ningún tipo de componente que pueda causar deformaciones en la forma del modo de pandeo. Esto significa que se debería de considerar{^F_glob} = {⁰}. En este caso Eq. (8) se escribiría de la siguiente manera:

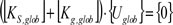
La Eq. (8) no significa que el modelo este descargado, sino que la carga no genera deformación en la forma del modo de pandeo (por ejemplo en el caso de pilares con carga axial pero no transversal). Dado que en las cercanías del punto de bifurcación del equilibrio {U_glob}≠ {0} , la condición de bifurcación se puede escribir como sigue:

En la práctica, en vez de la solución teórica de la Eq. (9), se puede aplicar el siguiente método numérico donde se asume que los resultados de tensiones son linealmente proporcionales al factor de carga λ, y en consecuencia la Eq. (5) se debe escribir como sigue:

En el punto crítico la segunda variación de la energía de deformación debería ser igual a cero (ya que el vector de carga no incluye ningún componente que genere trabajo externo).

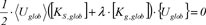
Eq. (11) se satisfice si:

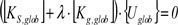
Introduciendo que A = [K_{S ,glob}], B = [K_{G ,glob}] es v = {U_glob} , la Eq. (12) se debe de escribir de la forma siguiente:

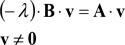
A este problema se le llama autovalores o valores propios y la solución numérica se resuelve en el software ConSteel en base al método de Lánczos modificado. Con este método se puede analizar un número arbitrario (como máximo el número de grados de libertad) de valores propios y vectores propios. El valor propio positivo más bajo dará el factor carga crítico, despreciando los valores negativos ya que no tienen un significado físico al no considerar el caso de inversión de carga.

La forma del modo de pandeo se determina con el vector propio apropiado. El software ConSteel aplica este método con gran precisión.

1.3.1 Ejemplo de pandeo lateral en viga mono simétrica

Seguidamente se calcula el valor límite de la carga transversal puntual aplicada en una viga simplemente apoyada con una sección transversal mono-simétrica (ala superior: 150-10,7; alma: 289,7-7,1; ala inferior: 75-10,7). La carga se encuentra en el medio de la sección trasversal y en el plano de simetría de la viga.

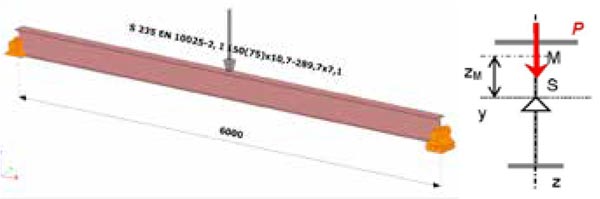
Solución teórica analítica

La ecuación general del momento crítico de pandeo lateral fue publicada por Clark and Hill (1960) y más tarde esta fórmula fue propuesta para utilizarla en el diseño por Boissonnade et al.(2006). La ecuación general es la siguiente:

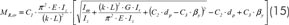
Donde d_p es la distancia entre el punto de acción de la carga P y el centro de esfuerzos cortantes M (esta es positiva, si la fuerza está dirigida a M mirando desde el punto de aplicación). El factor k=0,5-0,1 es el coeficiente de longitud de pandeo en el plano lateral de pandeo (0,5 es para extremos empotrados, mientras que1,0 para articulados). β_y, está relacionado con secciones mono simétricas y es positivo si la parte comprimida es el ala con mayor área:

Muchos investigadores han estudiado la calibración del coeficiente C y es posible encontrar un estudio amplio sobre estos factores en el libro de texto Silvaet al. (2013). El factor C para el modelo del ejemplo superior fue definido por Mohriet al. (2003) mediante una solución analítica con el siguiente resultado:

Debajo se muestran los detalles del cálculo para encontrar el momento crítico que está relacionado al valor máximo de la distribución de momento (en este caso el máximo se encuentra en el medio de la viga):

Solución con software ConSteel (método de elementos finitos):

La carga crítica para el modo de pandeo lateral se calcula mediante un modelo de elementos finitos de 7 GDL. Como M_cr=P_cr·L/4, se aplica una carga P=1/1,5 kN (de esta manera el momento crítico o es igual al valor propio). Los resultados se muestran en la Fig. 10. Llegando a las siguientes conclusiones:

Conclusiones: Se puede calcular la carga crítica de pandeo lateral con el software ConSteel con una buena precisión usando al menos n=2 elementos finitos por barra. La diferencia entre el momento crítico usando n=2 o n=32 es despreciable (menos del 0.6%).

1.4 Análisis de pandeo en sistemas de pórticos 2D

Una cuestión importante y motivo de debate científico o práctico, es el problema de la compatibilidad del alabeo en las esquinas de los pórticos. Aunque se han publicado diversos artículos técnicos en los últimos años relacionados con este tema (e.j. Camotim 2012)[5], no se conoce a día de hoy una solución analítica exacta para este problema, por eso, en esta sección se estudiará, con ejemplos numéricos, la precisión del método aproximado expuesto en los puntos anteriores.

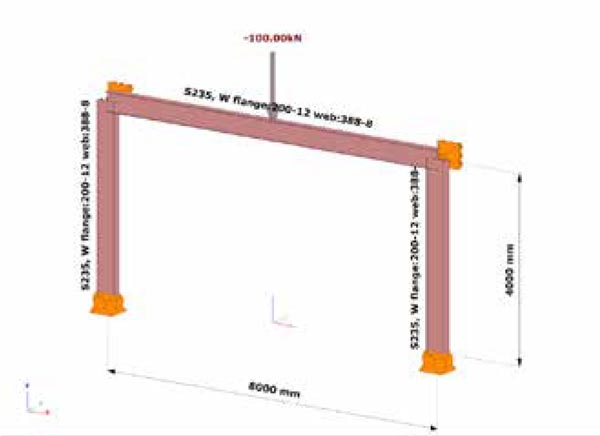
El modelo básico aplicado para el estudio de este efecto se muestra en la Fig. 11. donde los elementos de la estructura tienen secciones soldadas en I de inercia constante. La Tabla 5 muestra los tres sistemas de apoyos diferentes definidos en el pórtico. El sistema de apoyos S1 permite el modo de pandeo de la viga simple, mientras que el sistema S2 permite el modo de pandeo de columna simple. El sistema S3 permitirá un modo de pandeo de interacción entre viga y columna. Los modos de pandeo fuera del plano se analizan con elementos de 7 GDL (denominado como BC14 FE) y posteriormente con elementos placa tipo Shell MEF (denominado como shell3 FEM) para hacer un control y comparación.

Análisis con elementos de 7 GDL

Para el estudio del efecto de la definición de la trasmisión del alabeo entre elementos se utilizará dos modelos diferentes para los tres casos de apoyos definidos

• w_rígido (alabeo en extremo rígido): la estructura completa tiene una continuidad rígida entre barras para el grado de libertad del alabeo (excepto la base de la columna).
• w_libre (alabeo en extremo libre): se define en los extremos de los elementos de la estructura la condición de alabeo libre (no trasmisión de alabeo).

Análisis con elementos Shell FEM

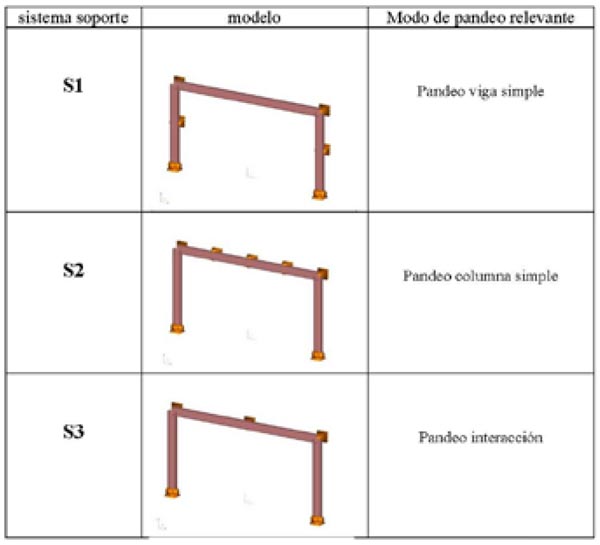
Para controlar la respuesta proporcionada por el modelo con BC 14 FE, se utiliza el método con Shell3 FEM para contrastar resultados y verificar la validez de los modelos. El nudo entre la viga y la columna en los modelos Shell3 FEM se debe de modelar como se muestra en la Tabla 6, donde se consigue una trasmisión más rígida en el alabeo mediante la introducción de placas de rigidización, así que se analizan varias soluciones constructivas del nudo para comparar con el modelo de barras BC 14 FE donde no se permiten condiciones intermedias en lo que se refiere a la trasmisión del alabeo entre barras (solo trasmisión total del alabeo o liberación total).

Conclusiones del estudio paramétrico:

Se calcula el factor de carga crítica de pandeo para cada modelo y configuración de sistema de soportes determinada por S1-S3, así como las 2 condiciones de enlace para el alabeo en los modelos de BC14 y las 4 configuraciones de nudos para los modelos de Shell3. Los resultados se muestran en la Tabla 7 obteniendo las siguientes conclusiones:

• El modelo con BC14 FE donde se define libre el alabeo en extremos de la viga (w_libre) ofrece una predicción segura y conservadora, excepto el caso de tipo de nudo J1 (nudos no rigidizados necesitan de un análisis con elementos Shell3 FE).
• El modelo con BC14 FE donde se define condición de continuidad del alabeo en extremos de la viga (w_ rígido) ofrece resultados seguros para nudos altamente rigidizados como el tipo J4. Para uniones parcialmente rigidizadas (e.j. J3) el modelo puede quedar por el lado de la inseguridad.

Sin embargo, se puede observar:

• Los modelos con BC14 FE ofrecen generalmente predicciones más seguras del comportamiento estructural que los métodos “manuales” utilizados tradicionalmente en la ingeniería estructural, donde las aproximaciones realizadas en los sistemas de apoyos y arriostramientos mediante la consideración de elementos equivalentes pueden tener un riesgo considerable.
• En situación de incertidumbre, el diseñador debe controlar la rápida solución con el uso de BC14 FE con modelos realizados mediante elementos Shell.

1.4.1 Ejemplo de un pórtico con perfiles de inercia variable

La Fig.12 muestra un pórtico simple a dos aguas con perfiles de inercia variable para vigas y columnas. Este ejemplo trata de mostrar el comportamiento fuera del plano en este tipo de estructuras para comparar los resultados entre los elementos barra de 7GDL y elementos placa tipo Shell.

Se analiza la estructura utilizando elementos BC14 FEM introduciendo la carga distribuida en la parte superior de las vigas. Los soportes laterales y puntos de apoyo se posicionan en el eje de referencia de las barras (el eje de referencia empieza en el centroide del extremo inferior y sigue paralelo a la ala exterior). Este modelo se compara con otro modelo idéntico en ConSteel pero utilizando elementos tipo Shell3 FEM donde se modelizan dos tipos de nudos para el estudio comparativo:

En la tabla 9 se muestran los resultados de cada modelo:

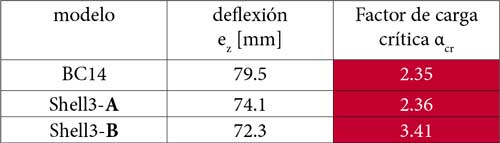
En la Fig. 13 se representan los modos de pandeo de los modelos utilizando elementos lineales BC14 y elementos placas Shell3-A, dónde podemos extraer las siguientes conclusiones:

• El modelo con elementos barra BC14 puede utilizarse de una manera segura para analizar el comportamiento fuera del plano en perfiles de inercia variable.
• El modelo de barras con BC14 puede predecir el comportamiento fuera del plano de perfiles de inercia variable para un amplio rango de sistema de apoyos.
• Cabe mencionar que los modelos con elementos placa Shell3 pueden obtener modos de pandeo locales en placas (abolladuras) y es por eso, que en algunos modelos, se pueden obtener resultados de cargas críticas más bajas que en los modelos de barras BC14 debido a este efecto, aunque este tema ya pasa formar parte del análisis de secciones clase 4.

1.5 Análisis del pandeo en modelos 3D

1.5.1 Introducción

Cada día es más habitual la realización de modelos 3D completos con gran detalle para realizar cálculos estructurales y verificaciones según distintas normativas, sin embargo, en la manera tradicional de tratar estos modelos, sólo se acaba utilizando el 3D para el cálculo de esfuerzos en todas las barras y no se aprovecha toda la definición geométrica del modelo para el diseño de la estabilidad de los elementos estructurales.

Esto es debido a que no se suelen realizar cálculos de “modos de pandeo global” en los modelos completos 3D donde éstos cálculos podrían reflejar la influencia que tienen algunos detalles constructivos definidos en el modelo analítico en la estabilidad de elementos, como es el caso de las excentricidades existentes entre barras, excentricidades en apoyos, posición exacta de las cargas etc. Es por este motivo, que los parámetros relacionados con la verificación de pandeo de elementos, como son los coeficientes β para el pandeo por flexión, o parámetros C para la verificación del pandeo lateral, se acaban calculando mediante tablas, libros o usando programas de cálculo especiales, para introducir estos parámetros, como información adicional, en los elementos estructurales del modelo 3D original para realizar verificaciones correctas a pandeo.

Este sistema de trabajo obliga al ingeniero a definir dos niveles de información en el software de cálculo, uno para el cálculo de esfuerzos (tipos de apoyos, condiciones de enlaces entre barras etc…) y otro para la definición de los parámetros de pandeo y estabilidad (coeficientes y longitudes de pandeo) para una correcta verificación según normativa, donde paradójicamente, los dos quieren reflejar una misma realidad.

Una manera de aprovechar todo el potencial de un modelo 3D definido en un software de cálculo además de para cálculo de esfuerzos, es mediante la realización de un análisis de estabilidad global sobre el modelo completo, donde los resultados de los modos de pandeo global, pueden reflejar el efecto que tiene la posición exacta de los perfiles en el modelo estructural (excentricidades), posición de arriostramientos e incluso el tipo de uniones entre elementos.

Seguidamente se explican algunas complicaciones que se pueden encontrar al tratar de realizar análisis globales de estabilidad en modelos 3D, para explicar en los puntos siguientes, herramientas para poderlos solventar como es el análisis parcial de valores propios (punto 1.5.2), o el estudio de sensibilidad al pandeo (1.5.3).

• Conflictos en la función principal de los diferentes elementos del modelo

Un problema elemental es que los modelos 3D contienen elementos de diferentes niveles pensando en su función principal dentro del análisis de pandeo:

• a) Elementos principales portantes: Pilares, Vigas, etc.
• b) Elementos secundarios y arriostramientos: cables de tracción, barras de compresión, o incluso las correas y el posible efecto diafragma de los cerramientos

El análisis global de pandeo se debe centrar en la evaluación de la estabilidad de los elementos principales o portantes aunque considerando los efectos de inmovilización provenientes de los sistemas de arriostramiento. Es por eso que los resultados de los modos de pandeo de los propios elementos de arrostramiento (irrelevantes para los elementos portantes), se deben filtrar de alguna manera para dejarlos fuera de los resultados del análisis.

• Precisión del modelo

Generalmente la precisión necesaria para el análisis global de pandeo requiere de la definición de un modelo estructural más fiel a la realidad que el habitual utilizado para el cálculo de esfuerzos únicamente. Esta precisión en el modelo está relacionada principalmente con la definición de la posición exacta de los elementos (excentricidades entre barras), cargas (aplicadas en ala superior o inferior del perfil) y los apoyos en su posición exacta. Además, se debería de tener en cuenta el comportamiento real de las uniones entre elementos no sólo en cuanto a la rigidez rotacional en el plano sino también fuera del plano de flexión, torsión y la continuidad del alabeo entre elementos conectados. Incluso en los casos donde los resultados del cálculo de los esfuerzos en los elementos no están influenciados por estas definiciones en el modelo, los resultados en los modos de pandeo global sí pueden ser muy sensibles a dichas condiciones.

• Modo de pandeo relevante

En un modelo estructural 3D es importante utilizar el modo de pandeo relevante y su carga crítica elástica correspondiente al elemento estudiado para su correcta verificación a pandeo. En el caso de modelos 3D estructurales complejos con muchas combinaciones de carga y un gran número de diferentes modos de pandeo, puede no ser evidente cual es el modo de pandeo más relevante a considerar para el diseño de los diferentes elementos.

Aunque puede que dependiendo de la estructura un análisis de estabilidad basado en el modelo global, no siempre sea la solución más directa y rápida, sí que en la mayoría de los casos ofrece una manera muy fiable y eficiente para el diseño, especialmente en aquellas situaciones donde tratar el comportamiento a pandeo de elementos de manera aislada al sistema real 3D (como se hace en la práctica) es incierta o incluso imposible en muchos casos. Este suele ser el caso típico cuando el modo relevante de pandeo es un caso espacial donde interaccionan diferentes elementos conectados entre sí. También, la evaluación de los modos de pandeo global en sistemas estructurales 3D, ofrece siempre una información muy valiosa al ingeniero acerca del comportamiento real de la estructura permitiendo hacer un análisis de optimización con más criterio que el habitual.

Esta sección está especialmente dedicada a mostrar las posibles soluciones a estos problemas teóricos con el fin de mostrar la eficacia y utilidad de calcular y verificar estructuras basándose en los análisis de estabilidad global en los modelos estructurales complejos 3D. En las siguientes secciones se presentan dos herramientas prácticas de análisis que demuestran cómo pueden ayudar a resolver los problemas descritos.

1.5.2 Análisis parcial de valores propios

Esta herramienta de análisis ofrece una solución al problema de conflictos en la función de los elementos. Tal y como se ha detallado en las secciones anteriores, la solución matemática más sencilla y robusta para los problemas de estabilidad en las estructuras metálicas es el análisis de valores propios de la ecuación Eq. (12). Cuando éste se aplica junto con el método de elementos finitos, el significado mecánico del valor propio (α_cr) es el factor de carga crítica elástica y (U_glob,i), el vector propio que está asociado al modo de pandeo del modelo estructural global. Sin embargo, en algunos casos sucede que, al introducir un modelo estructural completo, existen elementos en los que el ingeniero no está interesado en estudiar sus propios modos de pandeo (como los elementos de arriostramiento) ya que, además, al ser estas partes del modelo relativamente menos rígidas, aparecerían justamente en estos elementos los primeros modos de pandeo relevantes. Una situación típica es cuando se considera un sistema de correas en un modelo estructural 3D para tener en cuenta su efecto de arriostramiento en las vigas principales, y los primeros modos de pandeo que aparecen después de cálculo es el pandeo lateral de esas débiles correas. Para evitar estos casos y permitir al ingeniero concentrarse en el diseño de la estabilidad de los elementos portantes principales de la estructura, se puede definir un cálculo especial de valores propios llamado Análisis parcial de auto valores PEA (Partial Eigenvalue Analysis). Mediante el PEA es posible considerar que el modelo estructural se puede dividir en dos sub estructuras:

• (1) Subestructura relevante al pandeo (buckling relevant substructure (brs)) – aquellas partes del modelo donde interesa conocer los modos de pandeo y se deben de analizar (estructura primaria);
• (2) Subestructura irrelevante al pandeo (buckling irrelevant substructure (bis)) –aquellas partes del modelo donde no interesa analizar sus modos de pandeo pero sí considerar su efecto inmovilizador – su rigidez – (estructura secundaria y arriostramientos).

De acuerdo con el PEA la fórmula original de la Eq. (12) se rescribe como sigue:

Donde los nuevos términos significan lo siguiente:

• Kg,_brs  —–> La matriz de rigidez geométrica de segundo orden realizada sólo para la subestructura relevante al pandeo
• α_cr,brs,i  —-> i-th factor parcial de carga crítica elástica
• U_brs,i  ——> i-th modo de pandeo parcial

En una interpretación mecánica, el PEA permite obtener unos modos de pandeo especiales que están inducidos por las fuerzas internas que actúan sólo en los elementos que forman parte de la subestructura relevante, mientras que la rigidez inicial del modelo completo se considera como una condición de soporte para la subestructura relevante. En este sentido esta solución es similar – pero más precisa – que aplicar muelles elásticos ficticios en las partes de unión de la subestructura relevante modelada como soporte del resto de la estructura completa. La precisión mecánica de este método depende en gran medida en la selección de la subestructura relevante al pandeo. Un modo de pandeo parcial con su factor de carga crítico elástico es suficientemente preciso, si se puede obtener el mismo modo y factor del análisis de valores propios en el modelo global. Consecuentemente el error matemático (δ) del PEA puede expresarse como sigue:

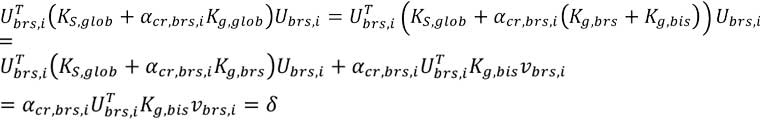
Mecánicamente este término de error expresa el trabajo de deformación realizado por la subestructura irrelevante al pandeo cargada en el vector desplazamiento del modo parcial de pandeo.

1.5.3 Análisis de Sensibilidad al Pandeo (Buckling Sensitivity Analysis BSA)

Esta herramienta de análisis ofrece una solución al problema para detectar el modo de pandeo relevante para cada elemento de la estructura, ya que esta labor es siempre responsabilidad del ingeniero de la misma manera que lo es la definición de longitudes efectivas de pandeo en los cálculos convencionales. Aunque la visualización de los modos de pandeo calculados es una muy buena ayuda informativa, el BSA permite conocer con un criterio más sólido la selección correcta del modo, ya que proporciona una visión muy valiosa en la importancia de los diferentes modos en los diferentes elementos.

Como medida fundamental, el BSA utiliza la energía de deformación interna generada por el modo de pandeo actual i-th (notaciones de la Eq. (12)):

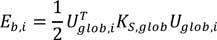
Usando esta medida, se puede definir un factor de relevancia del modo (mode relevance factor MRF) el cual indica cual es el elemento (k) relevante (crítico) para el modo de pandeo i-th de una determinada combinación de cargas. La base del cálculo de este factor es que cada modo de pandeo tiene uno (o varios) elementos que son los más críticos y a partir de allí todos los demás  elementos del modelo se comparan con el elemento más crítico para valorar la contribución que tienen en el pandeo:

Al elemento más crítico, este factor siempre toma el valor de 100%, y cuanto más cerca está el MRF de otro elemento al 100% más crítico será. Este factor puede aportar información al ingeniero para ayudarle a seleccionar los modos de pandeo relevantes para el diseño de estabilidad de elementos en modelos complejos 3D con diferentes combinaciones de cargas.

1.5.4 Ejemplo de análisis de sensibilidad al pandeo en pórticos

Para ver alguna de las aplicaciones de un estudio de sensibilidad, se plantea el cálculo de las longitudes de pandeo de los diferentes pilares del caso de la Fig.14 suponiendo una carga uniforme vertical en las vigas de 30 kNm. Una opción muy conocida es la utilización de ábacos como los de Wood, pero éste está sujeto a unas hipótesis que muchas veces no se dan en la práctica (como es el caso), luego se plantea un análisis de modos de pandeo y cargas críticas en el plano con el software ConSteel.

Una vez realizado el cálculo de cargas críticas y modos de pandeo, es posible ir visualizando en el programa cada uno de ellos. Observando el primero (el que da un factor da carga crítica de pandeo más bajo) podemos extraer las siguientes conclusiones:

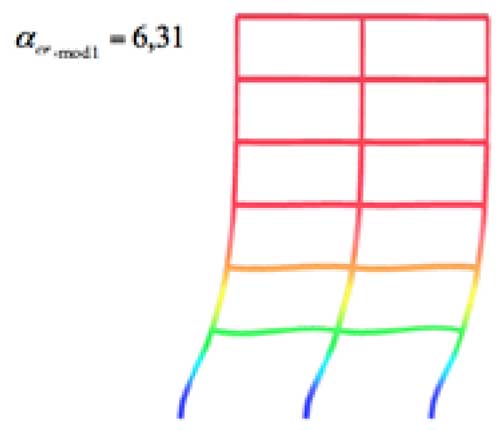
• El factor de carga crítica de pandeo es inferior a 10, con lo cual según EN 1993-1-1 (5.2.1)(3) el pórtico se clasifica como traslacional para un análisis global elástico.
• En este modo de pandeo, puede apreciarse claramente que no todas las columnas pandean simultáneamente (hipótesis básica del método de Wood ver Fig. 14).

De la forma de este primer modo de pandeo, se observa que sólo las columnas de la primera planta están fuertemente relacionadas con este modo de pandeo, luego se podría pensar que es correcto utilizar este factor de carga crítica para obtener las longitudes de pandeo de estas columnas según las relaciones siguientes:

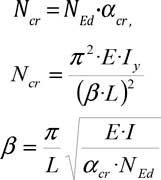
Donde:

• N_Ed  —–> Es el axil del pilar obtenido del cálculo de esfuerzos.
• α_{cr, mod1}  —–> Es el factor de carga crítica asociado al modo de pandeo

Sólo con la visualización de la forma de los modos de pandeo, aparecen ciertas dudas de si debemos utilizar este primer factor de carga crítica para calcular las longitudes de pandeo de las columnas de la segunda planta, aunque viendo la forma de este primer modo de pandeo, sí que queda claro que no será correcto utilizarlo para calcular las longitudes de pandeo de las columnas de las plantas más elevadas, ya que no sufren deformación alguna para este modo. Es por eso, que si queremos calcular las longitudes de pandeo en las columnas de las plantas superiores será necesario utilizar la información de los modos sub siguientes de pandeo con factores de carga crítica superiores como se muestra en la Fig. 16.

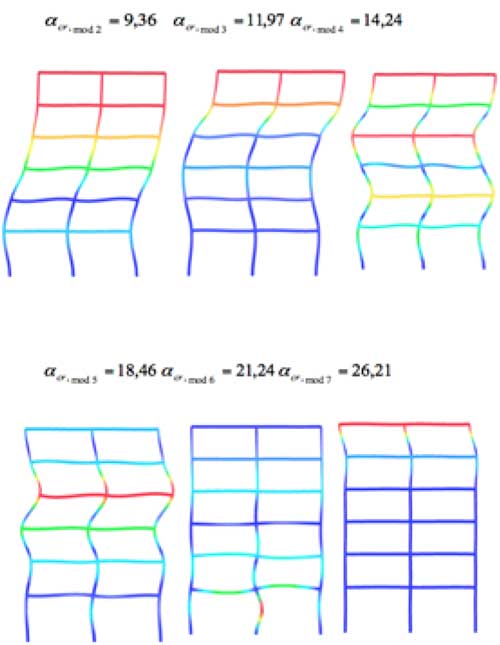
Por ejemplo, si queremos analizar el pandeo las columnas en la planta más elevada, no es hasta el séptimo modo de pandeo que se aprecia una deformación relevante de éstas columnas, con lo cual se podría pensar que se debería utilizar este factor de carga crítica de pandeo para conocer la longitud de pandeo de dichos pilares.

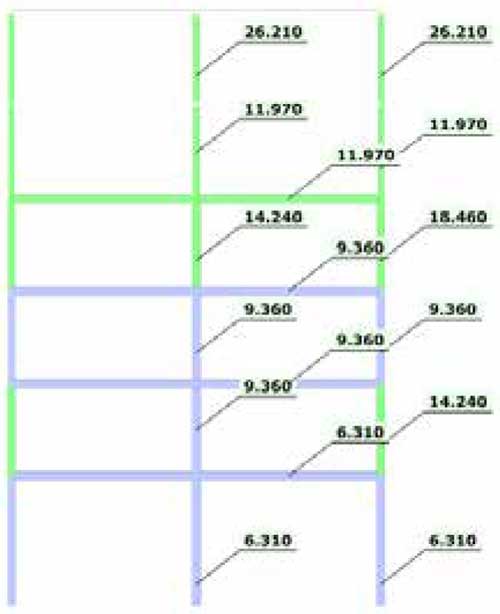
Como puede ser complejo que el ingeniero revise todos los modos de pandeo hasta encontrar los modos relevantes para las barras a estudiar sin un criterio más sólido, y además esto se puede complicar si tenemos varias combinaciones de carga diferentes, es de gran utilidad el análisis de sensibilidad al pandeo basado en la energía de deformación realizado por ConSteel, donde para cada modo de pandeo, el programa calcula el factor MRF para detectar la relevancia que tiene ese modo en la barra en cuestión. En la Fig. 17, se muestran los resultados de estos porcentajes para el primer modo de pandeo y para el séptimo, y como puede apreciarse, para el primero son las columnas del primer piso las que toman un porcentaje relevante de MRF (100% la columna central; 59.76% las exteriores y 49,44% la viga), pero no toman un porcentaje relevante las columnas del segundo nivel (apenas un 14,42% la central y un 5,64% la exterior). Para el modo de pandeo nº7 puede verse como son las columnas superiores las que toman un índice mayor de MRF (100% la columna central, y 48% las exteriores).

Finalmente, la utilidad de este estudio de sensibilidad viene con la posibilidad de realizar un filtro automático donde se le puede indicar al software ConSteel que tome para cada barra el modo de pandeo con un factor crítico más bajo donde su porcentaje de MEF afecte al menos en un determinado porcentaje, (por ejemplo el 25% es un valor a partir del cual ya se puede considerar que el modo de pandeo es relevante para esa pieza), de esta manera el software mostrará para cada barra el factor de carga crítico asociado con ese criterio, útil para conocer las longitudes de pandeo de todas las barras según Eq. (22).

2. Verificación de la estructura a partir de los modos de pandeo global

2.1 Principio del “método general” definido en el Eurocódigo

Esta sección trata de explicar mediante un ejemplo realizado con el software ConSteel, la aplicación del llamado “Método General” definido en el Eurocódigo EN 1993-1-1 (6.3.4), el cual utiliza los modos de pandeo global relevantes y sus factores de cargas críticas asociados, para la verificación de la estabilidad fuera del plano del modelo estructural. El ejemplo siguiente muestra una columna HEA200 de acero S235 JR simplemente apoyada con una restricción lateral en la mitad de su altura que impide también la torsión en ese punto (Fig. 19 a)). La columna está sujeta a una carga de compresión y a una carga distribuida definiendo una excentricidad para que actúe en el ala. En la Tabla 10 se muestran los pasos para el cálculo de la resistencia al pandeo (interacción del pandeo por flexión, y el pandeo lateral) usando el método clásico (basado en el tratamiento separado de los modos de pandeo aislados) y el método integrado basado en el “Método General”. Para el “Método General” se aplica una imperfección inicial en el plano de flexión para incluir el efecto amplificador que tiene carga de compresión en segundo orden en la flexión respecto al eje fuerte del perfil.

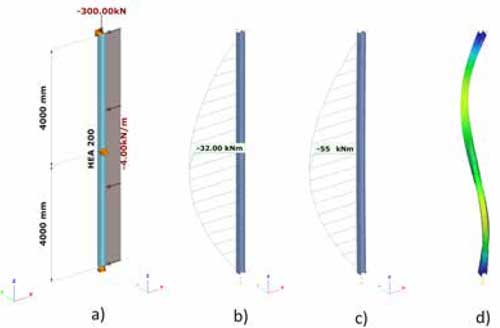
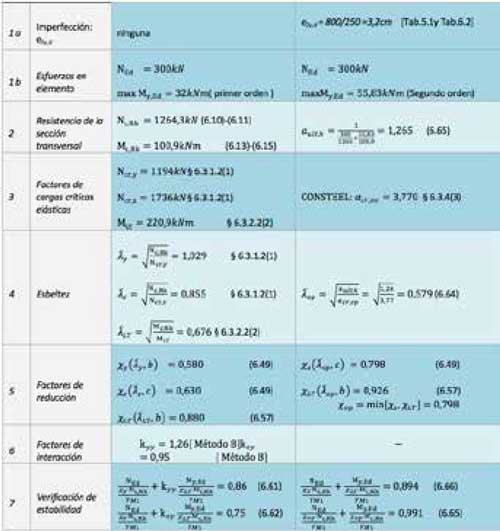
Se puede apreciar que la diferencia básica reside en el cálculo de las cargas críticas elásticas (paso 3) donde el método integrado no trata el efecto del pandeo por separado y utiliza el sistema completo para la determinación del modo de pandeo combinado (ver Fig. 19d) obteniendo un factor de carga crítico que naturalmente incluye todas las interacciones entre los diferentes efectos de las cargas en el pandeo. Consecuentemente sólo un valor de esbeltez describe el problema del pandeo sin la necesidad de buscar factores de interacción, ofreciendo una verificación final del perfil  muy similar al método clásico. Sin embargo, la gran ventaja del método general es que se puede utilizar del mismo modo para cualquier caso de carga y cualquier condición de soportes, eliminando por completo las incertidumbres que conlleva tratar separadamente los modos de pandeo aislados para luego tener que determinar longitudes de pandeo, parámetros del gradiente de momentos en los factores de interacción etc…

El método general del Eurocódigo permite escoger (en función del anejo nacional) entre la fórmula 6.65 o 6.66 para la verificación de la sección. Véase que la fórmula 6.66 (más precisa) ofrece prácticamente los mismos resultados que el método clásico 6.61, con la gran ventaja que el método general permite al ingeniero verificar elementos directamente de los resultados de los modos de pandeo obtenidos con un software como ConSteel, pudiéndose aplicar también en casos donde el método clásico no es directamente aplicable como:

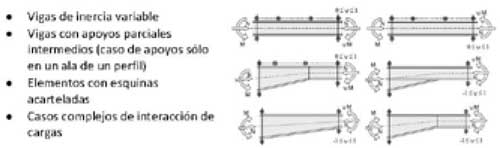
2.2 Aplicación del método General a un pórtico de Inercia Variable

En este ejemplo se utiliza el “Método General” para verificar la resistencia al pandeo fuera del plano en un pórtico 2D de inercia variable, mediante la utilización de elementos barra especiales de 7GDL con el software ConSteel. La geometría y la carga en la estructuras se muestran en la Fig. 21 donde se trata de reproducir las condiciones reales, definiendo en el modelo de cálculo, una excentricidad en la carga para que ésta actúe en el ala superior del perfil, y también definiendo excentricidades en los apoyos laterales respecto a los ejes neutros del perfil, para posicionarlos allí donde se encuentra el sistema de arriostramiento en la construcción real, incluyendo unos tornapuntas en la parte de esquina en las vigas y la parte mitad de las columna.

Para simplificar el problema, se aplica a todos los perfiles una altura variable de 900mm a 300mm con alas de 300mm de ancho por 16mm de espesor y 8mm de espesor de almas.

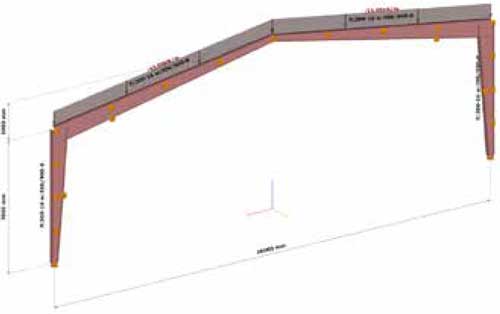
Seguidamente se detalla los pasos del método general realizado con el software ConSteel.

Paso 1: Cálculo del factor de amplificador de carga. Primeramente se realiza un análisis estructural en segundo orden definiendo un desplome de φ=1/200 (imperfección global) para obtener los esfuerzos y las tensiones elásticas en las secciones, luego se determina la sección más crítica para obtener el factor de amplificación de cargas αult más bajo en todo el pórtico.La sección crítica se sitúa la parte superior derecha de la columna:

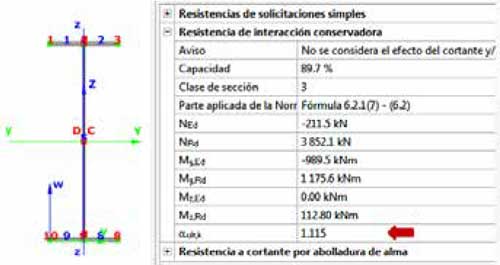
Paso 2: Calcular el factor de carga crítico de pandeo. Se ejecuta el cálculo de factores de cargas críticos de los diferentes modos de pandeo y el programa escoge el valor propio positivo más bajo relacionado con el modo de pandeo fuera del plano para determinar α_cr.op.

Paso 3: Calcular la esbeltez reducida fuera del plano. Usando los amplificadores de carga determinados en el Paso 1 y el Paso 2 se puede calcular una esbeltez global como sigue:

Paso 4: Calcular los coeficientes de reducción. Usando la esbeltez reducida calculada en el paso 3, se calcula los factores de reducción para pandeo por flexión alrededor del eje débil del perfil χ_z y el factor de reducción para el pandeo lateral χ_LT.

Paso 5: Verificar la Resistencia al pandeo Se verifica la resistencia a pandeo fuera del plano del pórtico a partir de esfuerzos en la sección crítica mediante la fórmula de interacción conservadora.

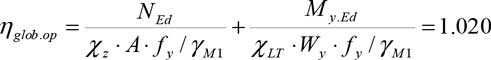
Paso 6 (Opcional): Excluir las zonas de unión en la verificación de la barra.

Para un cálculo más preciso, existe una función especial en ConSteel, que permite excluir la zona de unión de esquina donde en realidad no existe un elemento viga hasta el punto de encuentro teórico, sino una zona de unión que se normalmente se analiza de manera especial en el proceso de cálculo de la unión. Así que el software permite considerar en los cálculos esa zona como rígida teniendo una ligera influencia en el resultado de modos de pandeo, esfuerzos y lo más importante, la obtención de αult, y verificación inmediatamente fuera de la zona de unión y no en un punto de encuentro teórico.

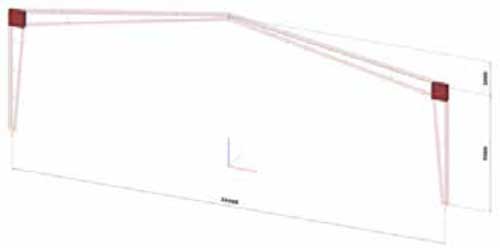
Los resultados del cálculo con esta consideración son:

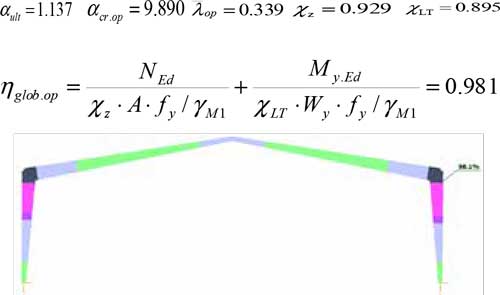
Conclusiones

• El “método general” especificado en EC3-1-1 6.3.4 se puede aplicar directamente a pórticos planos de inercia variable de una manera directa y sencilla.
• Los apoyos laterales en sus posiciones reales tienen un efecto directo en la verificación final del pórtico sin la necesidad de calcular ni introducir longitudes de pandeo ni coeficientes de gradientes de momentos para el pandeo lateral.

2.3 Aplicación del método General a un sistema 3D

En este ejemplo se presente un análisis 3D completo de una construcción industrial. La estructura consiste en 5 pórticos internos con refuerzos en las esquinas y 2 pórticos hastiales menos reforzados y un sistema de arriostramiento (barras tipo tirantes y elementos de compresión) conectados de manera excéntrica a los elementos principales como nuestra la Fig. 28. En la parte superior de las vigas, se ha considerado la rigidez elástica rotacional proporcionado por el sistema de cubierta formado por correas y cerramiento Kindmann, R [10], aplicando muelles rotacionales elásticos. Las cargas se han modelado como cargas superficiales 3D actuando en la cubierta y en todas las paredes de la estructura, ver por ejemplo las cargas de viento en la Fig. 29 donde estas cargas superficiales se reparten de manera automática a cargas lineales en los elementos según su superficie tributaria.

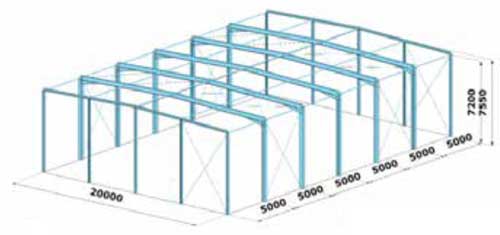
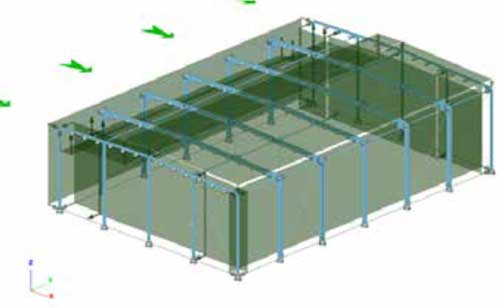
Para analizar la estabilidad de los pórticos en este modelo complejo 3D, se realiza primeramente un análisis de pandeo para el modelo completo (Global Eigen value Analysis (GEA)). En la Fig. 30.a se puede ver el modo de pandeo dominante a α_cr= 1,76y en la Fig. 30.bel MRF asociados para las vigas y columnas a ese modo de pandeo. El MRF muestra que los elementos dominantes en el modo de pandeo global son las vigas de la derecha y además, debido a los efectos espaciales, el tercer pórtico es el elemento más dominante – y esto está en consonancia con la representación de los modos de pandeo.

Para estudiar con más detalle la influencia de los diferentes modelos simplificados que uno puede tratar en el problema del pandeo, se realiza un Análisis Parcial del Pandeo (PEA) de 4 subestructuras dentro del modelo 3D:

• Modelo parcial 01 – todos los pórticos internos: Fig. 31 a)
• Modelo parcial 02 – sólo el tercer pórtico: Fig. 31 b)
• Modelo parcial 03 – todos los pilares interiores: Fig. 31 c)
• Modelo parcial 04 – todas las vigas interiores: Fig. 31 d)

Además, para comparar con el método tradicional donde se verifica el pandeo en los elementos de manera aislada, se realizan dos modelos aislados para la viga y columna:

• Modelo aislado de la columna: Fig. 32 a)
• Modelo asiladode la viga: Fig. 32 b)

En la Fig. 31. Se pueden ver los modos de pandeo con sus factores de cargas críticos y en la Tabla 1 se comparan todos los diferentes tipos de análisis al pandeo:

Los resultados muestran que el cálculo de los pórticos de manera separada o de sólo un pórtico, no causa error en el análisis de estabilidad, sin embargo, aislar las columnas o las vigas puede traer resultados incorrectos para niveles de carga próximos al pandeo. Esto sucede al tratar el pandeo de elementos por separado cuando éstos en realidad contribuyen en un mismo modo de pandeo global combinado. Además, también se puede ver que los modelos parciales PEA de sólo las columnas (modelo 03) y el de sólo las vigas (modelo 04) dan factores de carga críticos superiores a los modelos parciales de los pórticos (modelo 01 y 02) y este hecho indica nuevamente que es un error considerar esos modelos aislados para el pandeo (modelos 03 y 04). Para este caso también se puede ver que tratar la viga de manera aislada ofrece un resultado algo más conservador que hacerlo según el modelo parcial 01, y que tratar la columna de manera aislada puede acarrear resultados inseguros ya que este modelo ofrece un factor superior de carga crítica al modelo parcial 01.

Seguidamente se aplica el método general para los siguientes modelos:

Verificación de la estructura utilizando el factor de carga crítico del Modelo completo 3D

Seguidamente se aplican las ecuaciones Eq. (23) y Eq. (24) considerando α_cr= 1,76 obtenido en el cálculo de modos de pandeo del modelo completo y α_ult mínimo para cada barra.

Este mismo porcentaje se encontraría utilizando el modelo parcial 01 ya que αcr es prácticamente el mismo (α_cr1,77)

Aplicando el método general se encuentra un factor de utilización del 111,8% en la parte superior de la columna y 100% en la viga, luego la columna no cumpliría.

Verificación de la estructura utilizando los modelos aislados

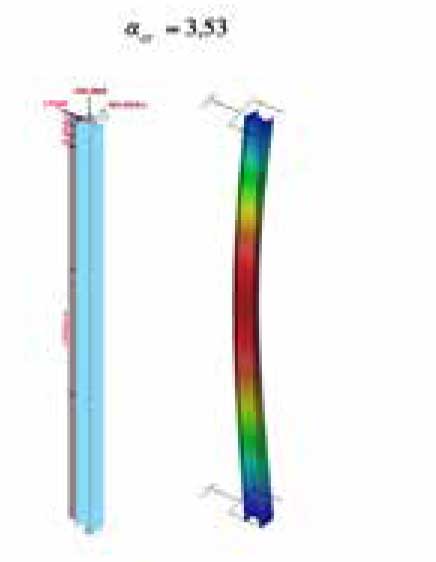
Aplicando el método general pero considerando los factores de carga críticos de los modos de pandeo de los elementos obtenidos de manera aislada mostrados en la Fig. 32a y 32b (tal cual hace la normativa), se obtienen los siguientes porcentajes en las verificaciones:

Puede verse que para este caso, el considerar las barras de manera aislada ofrece resultados muy parecidos en la viga pero ligeramente diferente en la columna, y esto es debido a que el método aislado en la columna no considera el modo de pandeo de interacción con la viga (αcr Columna aislada = 3.53 y αcr del sistema columnaviga= 1.77).

Conclusiones

• El “método general” se puede aplicar de manera rápida y sencilla en modelos completos sin la necesidad de introducir longitudes de pandeo ni parámetros para pandeo lateral obteniendo resultados del lado de la seguridad.
• El método es aplicable para perfiles acartelados o de inercia variable.
• El método es especialmente útil para casos donde las condiciones de los extremos de los elementos son difíciles de valorar, o cuando el modo de pandeo no se puede aislar debido a que interaccionan más elementos conectados.

Aunque este ejemplo pretende resaltar la diferencia existente entre el diseño basado en el método tradicional  y el método basado en el estudio detallado de los modos de pandeo, modelos más precisos en ConSteel suelen permitir una mejor optimización de la estructura.

3. Bibliografía

Referencias bibliográficas

[1] Borsoum and Gallagher (1970): Finite Element Analysis of Torsional and Torsional-Flexural Stability Problems, International Journal for Numerical Methods in Engineering, Vol. 2. 335-352, Wiley & Sons 1970
[2] Chen and Atsuta (1977):Theory of Beam-Columns. Vol.2: Space Behaviour and Design, McGraw-Hill, 1977
[3] Kindmann and Kraus (2007): Finite Element Methoden im Stahlbau. Berlin: Verlag Ernst & Sohn 2007.
[4] Turkalj et al. (2003): Large rotation analysis of elastic thin-walled beam- type structures using ESA approach, Computers & Structures 81 (2003)
[5] C. Basaglia, D.Camotim, N.Silvestre (2012): Torsion warping transmission at thin-walled frame joints: Kinematics, modelling and structural response. Journal of Constructional Steel Research 69/1
[6] Clark and Hill (1960): Lateral buckling of beams. Proc. ASCE, ST7, 175-190
[7] Boissonnade et al. (2006): les for Member Stability in EN 1993-1-1, Background documentation and design guidelines, ECCS Technical Committee – Stability, No 119, 2006 ISBN 92-9147-000-84, p. 229
[8] Silva et al. (2013):Comparison between C factors for determination of the elastic critical moment of steel beams, ECCS Technical Committee – Stability, Working Paper for Meeting in Stuttgart, Germany 21 June, 2013
[9] Mohri et al. (2003): Theoretical and numerical analyses of unrestrained, mono-symmetric thinwalled beams. Constructional Steel Research 59 (2003), pp. 63–90.
[10] Kindmann, R: Stahlbau, Teil 1:Grundlagen. Berlin: Verlag Ernst & Sohn 2013.