Una estàtica recíproca

JOSEP M. GENESCÀ RAMON
Consultor d’estructures i geòmetre.

L’extraordinària influència que les estàtiques gràfiques de Culmann i Ritter van tenir posteriorment en el càlcul d’estructures no s’entendria sense la col·laboració d’uns personatges savis. Van ser fonamentalment tres: Rankine, Maxwell i Cremona. Contemporanis, però desvinculats entre ells, amb dedicacions professionals i acadèmiques en les quals l’enginyeria estructural és marginal, coincideixen exposant una filosofia geomètric-estructural amb criteris de reciprocitat.

Això permet un desenvolupament ràpid dels mètodes gràfics de càlcul estructural. Després d’una introducció en què es clarifica el significat de l’estàtica reciprocista, tant des del punt de vista geomètric com estàtic, s’exposaran aquí, de forma exclusivament gràfica, les investigacions dels autors abans indicats amb la intenció de clarificar i col·locar en el seu context històric una qüestió tan important com poc estudiada.

CONTEXT HISTÒRIC

La història ens ensenya que enfront d’una demanda social, econòmica o d’altre tipus, la ciència intenta donar resposta a aquesta demanda. Per exemple, els mètodes iteratius per resoldre estructures hiperestàtiques apareixen quan es dona l’erupció del formigó armat.

De la mateixa manera, l’extraordinari desenvolupament del ferrocarril a la primera meitat del segle xix obliga a resoldre uns problemes amb urgència. La topografia d’alguns indrets, especialment les depressions i els rius, obligava a la construcció de ponts que s’havien prèviament de projectar i calcular. Ja es disposava del material, el ferro. Però era necessari un instrument que permetés, d’una manera compatible amb la urgència social de l’època i esquivant els plantejaments analítics complicats i laboriosos, el dimensionament dels diversos elements que els formaven. D’aquesta manera van sorgir Rankine, Maxwell i Cremona amb una proposta reciprocista que es convertia en l’instrument més apreciat a mitjans del segle xix. Es van alimentar intellectualment, per una part, de la geometria descriptiva de Gaspar Monge i dels coneixements grafostàtics de Jean Poncelet i van establir amb els seus estudis sobre figures recíproques els criteris fonamentals perquè Karl Culmann pogués donar a l’estàtica gràfica en primer lloc, i al polígon funicular posteriorment amb Wilhelm Ritter, tota la dignitat intel·lectual necessària.

INTRODUCCIÓ

Es diu que una figura és recíproca d’una altra quan entre les dues es pot establir una relació biunívoca de relacions o propietats.

El Diccionari de la Llengua Catalana defineix ‘Reciprocitat’ com «Fet per dos l’un a l’altre, donat i rebut alhora per cadascun de dos», altres diccionaris aposten per identificar la reciprocitat amb la bilateralitat. Matemàticament, si a i b són dos números i es dona que a · b 5 1, és a dir, que recíprocament els dos números executen la mateixa acció sobre l’altre, cadascun per l’altre es dirigeixen a la unitat i formen un conjunt de recíprocs. El terme ‘Reciprocitat’ o els seus sinònims o antònims (correspondència, intercanvi, permuta, correlació, etc.) són utilitzats en diversos camps expressant diversos conceptes segons la matèria a la qual vagi dirigit el terme. Per exemple, en química inorgànica es parla de ‘Poliedres recíprocs’, també s’utilitza la reciprocitat en antropologia cultural i en psicologia i altres qüestions com la reciprocitat de veus o temes relacionats amb el llenguatge. Però fixem l’atenció en les matèries que parlen de reciprocitat més o menys relacionades amb l’arquitectura o les estructures.

En geometria es diu que ‘Poliedres recíprocs’ són aquells en què els vèrtexs d’un coincideixen recíprocament amb les cares de l’altre. A la figura 1, el cub i l’octaedre son recíprocs.

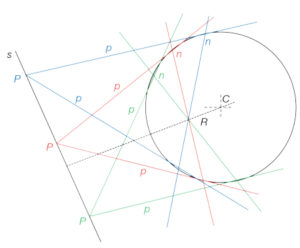
Gaspard Monge (1746-1818) en la Géométrie Descriptive de 1798 parla d’un concepte molt interessant, la ‘Reciprocitat polar’. Si es té una circumferència de centre C i des d’una recta qualsevol s es llancen des dels punts Pi (P, P, P…) tangents a la circumferència (p, p, p…) i unim els punts de tangència (n, n, n…) amb rectes, aquestes es troben en un sol punt R i es dona que la prolongació de la recta C-R és perpendicular a s. Si els punts Pi estan a la polar de R, recíprocament R està a la polar dels punts Pi (fig. 2).

James Maxwell (1831-1879) publica al 1864 l’anomenat ‘Teorema dels desplaçaments recíprocs’ on s’anuncia que, si una sol·licitació actua en un punt A d’un cos elàstic, la deformació que es produeix en un altre punt B del mateix cos és igual, recíprocament, a la que es produiria en A si la sol·licitació es dona en el punt B.

Una ‘Estructura recíproca’ és un muntatge en l’espai on els elements que la formen se suporten mútuament, o es necessiten mútuament, de manera recíproca, per aconseguir l’equilibri. Perquè això sigui possible és necessària l’existència d’un estat de fregament entre les peces.El menor nombre d’elements és tres i cadascun d’ells s’entrega en el següent fins que l’últim coincideix amb el primer. La reciprocitat a les estructures està estudiada des de fa molt de temps, atès que permet realitzar cobertes de forma relativament fàcil i econòmica (fig. 3).

El març de 2017 Jorge Blasco, membre de l’ACE, pronuncia un conferència il·lustrativa i rigorosa sobre el tema.

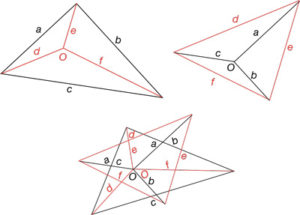
Simplificant, per exemple, en el cas de figures en el pla (però també en l’espai), es dirà que són recíproques si una d’elles és un polígon tancat i l’altra, construïda amb les paral·leles (o perpendiculars) a la primera, coincideixen en un punt O (reciprocitat geomètrica) (fig. 4).

El conjunt de dues figures recíproques més elemental és el triangle o una figura composta per triangles (fig. 5).

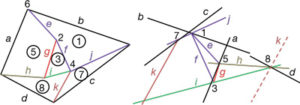
Les figures recíproques poden complicar-se tant com es vulgui. A la figura 6 es realitza un procés de complexitat creixent que es concreta assignat un color diferent per a cada dualitat recíproca. Per exemple, el punt format per la trobada de les línies g-h-i es reprodueix amb triangles recíprocs a partir de la segona construcció.

No totes les figures tenen la seva recíproca. A la figura 7, tancada i amb 11 línies, s’aconsegueix la reciprocitat als set primers temptejos però és a la vuitena on el polígon tancat d-h-i-k, designat amb el número 8, no té reciprocitat, atès que les línies d, h i i es troben en un punt, designat de la mateixa forma amb el número 8, però es dona la impossibilitat que la línia k coincideixi amb les altres tres, ja que forma també part del triangle c-j-k i del punt 7 a la figura recíproca.

Esbrinem quin significat estàtic pot tenir aquest concepte geomètric de reciprocitat. O com la geometria i l’estàtica poden compartir una reciprocitat. Si suposem que les línies coincidents en el punt O (fig. 8) són barres, en principi coplanàries i sense pes propi, aleshores aquest punt de coincidència pot ser un nus estructural. Sobre les barres que el formen es poden transmetre forces de determinada intensitat i sentit.

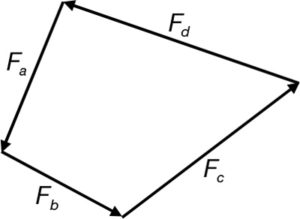
Aquestes forces poden equilibrar o no el nus. Per comprovar l’equilibri podem senzillament aplicar la llei del paral·lelogram amb les forces Fa i Fb i la resultant a la següent Fc i així successivament i amb l’ordre que es consideri oportú fins obtenir la resultant Fa 1 Fb 1 1 Fc, que comprovem té la mateixa intensitat i sentit contrari que Fd. En aquest cas el nus està en equilibri (fig. 9).

Però era el cas d’una estructura molt senzilla. En altres casos, aquesta composició de forces es pot complicar excessivament.

Per il·lustrar la complexitat que l’aplicació de la llei del paral·lelogram té en alguns casos, observem el següent exemple. En aquesta estructura (fig. 10) es pot comprovar que la utilització de la llei del paral·lelogram per resoldre estructures compostes per barres en el pla i isostàtiques és extraordinàriament dificultós. Primerament, amb l’ajut del polígon funicular, s’han calculat les reaccions RA i RB. Començant pel nus compost per les barres 1-2-3 s’ha anat avançant fins arribar a la barra 9 on les dificultats gràfiques es fan excessives.

Però en tot cas és possible resoldre estructures d’aquest tipus sense recórrer a les qüestions reciprocistes, tot i que amb molta paciència. La contradicció de l’exemple és que s’ha utilitzat el polígon funicular per trobar les reaccions, que és un procediment reciprocista, per a continuació intentar resoldre els esforços a les barres amb la llei del paral·lelogram.

Si representem les forces aplicades a cada barra de la figura 9 en una altra figura a base de col·locar, una darrere de l’altra, les paral·leles de les forces del nus, tindrem un polígon de forces. Si l’origen de la primera força Fa coincideix amb el final de l’última Fd, direm que el nus O està en equilibri i que les dues figures, el nus i el polígon de forces, són figures recíproques (fig. 9).

A més, es comprova que polígons tancats a partir del traçat de línies paral·leles al nus són infinits, tant si es tracta de figures homotètiques (F9a…F9d) (fig. 12) o no (F 0a…F 0d) (fig. 13).

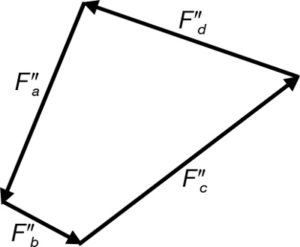
Evidentment, si el polígon no queda tancat (R produeix el desequilibri) no es dona l’equilibri i, a més, les dues figures formades no són estàticament recíproques (fig. 14).

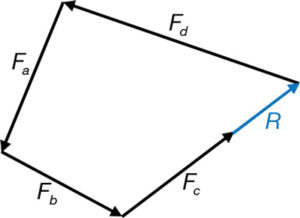
Aquí s’ha pogut comprovar la relació estàtica entre figures recíproques. La reciprocitat es dona no solament de forma geomètrica sinó també, i això és el que realment interessa, de forma estàtica. Per tant, de les dues figures recíproques, una representa geomètricament l’estructura i, l’altra, el conjunt de forces que permeten que la primera es trobi en equilibri.

Tornem a la figura complexa exposada anteriorment a la figura 6 i la considerem una estructura formada per les barres a…r en el pla i afectada de diverses forces en cadascuna d’elles. Aquestes forces es poden pre-dimensionar col·locant-les en el seu lloc i adoptant el nom de la barra on actua sense determinar la seva intensitat (fig. 15).

El polígon de forces ens donarà, per a cada barra i pel triangle corresponent, una de les infinites forces en la qual s’aconsegueix l’equilibri (fig. 16).

Finalment, aquestes forces es poden traslladar a l’estructura inicial per obtenir l’estructura en equilibri amb la sol·licitació a cadascuna de les barres (fig. 17). Per exemple, les forces Fp, Fq i Fr que es troben en un nus a l’estructura (fig. 17) formen un triangle en el polígon de forces (fig. 16).

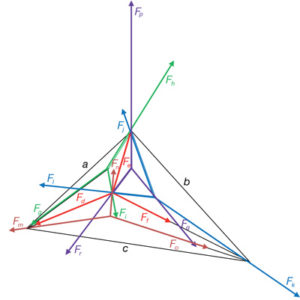
D’igual manera, en l’espai, es poden reproduir les mateixes disposicions recíproques.

L’estructura composta per triangles, treballada anteriorment, es pot considerar com la projecció ortogonal d’un poliedre irregular o piràmide en què el punt O és la projecció, en el pla de la base a, b i c, del vèrtex del poliedre (fig. 18).

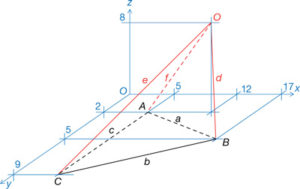
Col·locada en un espai de tres dimensions, a la figura determinada pel poliedre se li pot assignar una altra figura recíproca a base de transformar en punts les cares triangulades del poliedre i en cares o triangles, les arestes de la figura original. D’aquesta manera, els triangles o cares de la figura original a-b-c, e-f-c, f-d-a i e-d-b, en l’espai a la figura 19, es transformen, projectant-se ortogonalment i respectivament en els punts M, Q, P i R (en color negre les que es mantenen en el pla x-y i en color blau les que són projeccions en el pla x-y) (fig. 20). De la mateixa manera, els triangles b-c-e, a-c-f, a-b-d i e-f-d de la figura construïda com recíproca es converteixen respectivament en els punts C, A, B i O de la figura original.

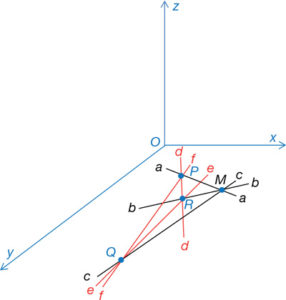
Es tracta, a continuació, d’aixecar el punt M que es troba en el pla de x-y a l’alçada que es cregui convenient, per exemple, el punt O (fig. 21). A qualsevol alçada es conserva el criteri de reciprocitat de forma que es poden trobar infinites figures recíproques a l’original. La figura 22 n’és una d’elles. A la figura 23 es fa coincidir el punt O en el pla x-y explicitant la reciprocitat de manera més gràfica.

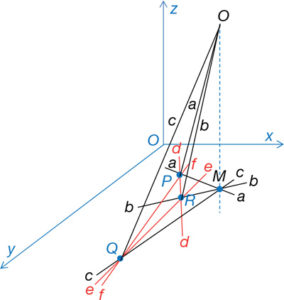
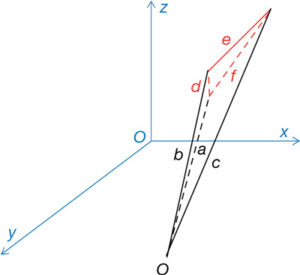
Per tant, es poden aconseguir infinites figures recíproques a l’original i a cada figura li correspondrà un equilibri de forces diferent. Sembla lògic, en conseqüència, tantejar una figura que permeti un estat de forces que sigui apte per a les necessitats en què es trobi la figura original o, en aquest cas, l’estructura original. D’aquesta manera, l’equilibri en el nus O (fig. 24) es dona per l’equilibri de forces en el triangle Fe, Fd i Ff de la figura recíproca, mentre que l’equilibri en el nus O (fig. 25) de la figura recíproca es dona per l’equilibri de forces Fa, Fb i Fc de la figura original. És un exemple de dualitat estructural aconseguida per reciprocitat geomètrica.

Maxwell en On Reciprocal Figures, Frames, and Diagrams of Forces cita dues vegades a Ranquine per ressaltar la seva proposta del poliedre de forces en el Philosophical Magazine de febrer de 1864. Rankine anuncia que si a les cares d’un poliedre se li associen forces perpendiculars a les esmentades cares i proporcionals a les seves superfícies, aquestes es troben en un punt i, per tant, estan en equilibri.

A continuació, es fa un resum de les aportacions que tant Rankine com Maxwell i Cremona fan a l’estàtica reciprocista¹. Es veurà que, en el fons, les aportacions són molt similars entre els tres, les diferències són de matís. Per facilitar les coses s’utilitzaran estructures i figures que, sempre que es pugui, siguin repeticions.

¹ No és fàcil llegir els seus escrits. En primer lloc, el lèxic és diferent i, en no existir la ‘Resistència de Materials’ com a tal, les paraules poden induir a error. Per exemple, s’utilitza la paraula ‘dual’ com a sinònim de ‘recíproca’ quan en realitat ambdues expressen conceptes diferents. També la dificultat d’impressió dels textos, en allò que es refereix als dibuixos, fa que hagin d’explicar amb paraules allò que fàcilment s’expressaria amb un dibuix, tot i que les planxes al final dels llibres intenten clarificar (de forma absolutament romàntica) aquestes coses. Tampoc el poc domini (o el meu poc domini) de les geometries de l’època, com la geometria projectiva, facilita les coses. Els tres savis estudien les forces estàtiques en l’espai. Com era d’esperar, Maxwell ho fa de manera analítica en un desenvolupament intricat, contràriament a allò que deia Culmann, que els mètodes gràfics permeten resoldre qüestions estructurals de forma gràfica, és a dir, sense haver de recórrer a grans plantejaments analítics. Aquesta era la idea fins al primer quart del segle xx.

RANKINE

William John Macquorn Rankine va néixer a Edimburg el 1820 i va morir a Glasgow el 1872. És el més jove dels investigadors que tractem en aquest estudi, tot i que entre ell i el més gran (Maxwell) es porten només 11 anys. Es pot afirmar, doncs, que es tracta de contemporanis.

Va ser matemàtic, enginyer i físic. Però com tots els grans personatges d’aquella època, va estudiar pràcticament tots els temes científics al seu abast. Tot i que la seva salut de nen i adolescent no li permetia una educació ordenada i completa va assistir a classes a l’Escola Superior de Glasgow i a l’Escola Naval, però va sortir de la Universitat d’Edimburg el 1838 sense cap grau. Finament va ser catedràtic d’Enginyeria Civil i Mecànica a la Universitat de Glasgow. Apart dels estudis sobre història i filosofia natural estudia la teoria ondulatòria de la llum, dissenya vaixells, com també dona a conèixer el ‘Mètode de Rankine’ per al traçat de corbes de ferrocarril. Però on s’identifica més és en els estudis de termodinàmica per al funcionament de la màquina de vapor ‘Cicle de Rankine’ i en l’estudi de mecànica del sòl, especialment de les sorres.

En allò que es refereix a la resistència de materials, el 1843 dona a conèixer una teoria de ruptura per fatiga dels eixos dels ferrocarrils, també una teoria de fallida sota càrrega estàtica i la plasticitat en estat límit coneguda com ‘Corba de Rankine’ i ‘Estat de Rankine’ respectivament. En el seu llibre Manual of applied Mechanic estudia el polígon funicular sense donar-li encara la rellevància històrica i pràctica que li donaria Culmann, però està clar que, encara que els seus estudis sobre estàtica no arriben a l’alçada ni de Maxwell ni de Cremona, no deixen de ser significatius. Rankine, de petit, tenia una gran tirada per la música, cosa que el va fer dubtar si dedicar-se a la matemàtica o a la música. Per això, i al llarg de la seva vida, es va dedicar a la música tant com va poder. Va ser cantant, pianista i violoncel·lista. De la mateixa manera que Maxwell va ser poeta i va editar la seva obra literària. Una manera absolutament rankineana de mesclar l’amor amb les integrals es troba en la novel·la The Mathematician in Love.

Rankine fa una proposta reciprocista conceptualment semblant a la que fa Cremona però de forma abstracta, amb poca aplicació pràctica, i almenys en els papers que ens han arribat, presentant els problemes al contrari d’allò a què estem acostumats.

Suposem tres forces formant un triangle en equilibri F1, F2 i F3 (fig. 26). Es tracta de forces abstractes desvinculades de qualsevol estructura. Des d’un punt qualsevol O tracem les línies a, b i c als vèrtexs del triangle de forces A, B i C (fig. 27).

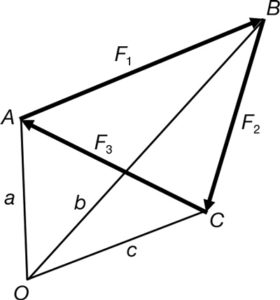
Si per reciprocitat tracem paral·leles a aquestes línies tindrem el triangle a, b i c (fig. 28). Si transformem aquest triangle en una estructura composta per barres indeformables, situada en el pla i de nusos articulats, aplicant-li les forces F1, F2 i F3 de tal forma que F1, a i b formin per reciprocitat F1, a i b, i el mateix amb les forces F2 i F3, tindrem que l’estructura a, b i c estarà en equilibri atès que F1, F2 i F3 també ho estan. Hem aplicat la reciprocitat tant a la geometria com a les forces. Els esforços que aquestes forces produeixen a les barres de l’estructura Fa, Fb i Fc són les distàncies, a escala de forces, de les línies a, b i c (fig. 29).

Quant al signe de les sol·licitacions a l’estructura: mirem, per exemple, el triangle F1, a i b de la figura 27 que es transforma per reciprocitat en el punt F1, a i b de la figura 28. El sentit de F1 ens donarà el de Fb i el de Fa. En aquest cas, la barra a es troba comprimida i la b traccionada². Igual podem operar amb les altres barres, tal com es veu a la mateixa figura 28.

² El sentit de les forces a les barres d’una estructura és marginal en la reciprocitat, però en tot cas, per observar el sentit de les forces que transcorren per les barres, es tindrà en compte que aquest sentit el dona l’equilibri dels nusos. Des d’aquest punt de vista, el sentit de les forces en una figura tancada sempre ha de ser el mateix (amb altres paraules, les fletxes o finals de les forces sempre van en el mateix sentit) i aquest és el que s’ha de traslladar a l’estructura. En aquesta, quan dos punts extrems d’una mateixa barra tendeixen a juntar-se, direm que la barra està traccionada, i al contrari, quan aquest dos punts tendeixen a separar-se, direm que està subjecta a una compressió. A la figura 39 es grafia el sentit de les forces d’un triangle segons una regla donada per Maxwell.

Si volem generalitzar les teories de Rankine, considerem una estructura composta per barres 1…6 en el pla i amb nusos articulats, com la que es veu a la figura 30. Si des d’un punt qualsevol O tracem paral·leles als costats de l’estructura, tindrem la primera reciprocitat, atès que en el punt O es troben les línies 1…6 (fig. 31). Entre dues línies amb vèrtex comú de l’estructura, per exemple, la 1 i la 2 i que en el polígon recíproc s’identifiquen com 1 i 2, tanquem el triangle amb una força qualsevol com F1. Efectivament, F1, 1 i 2 formen una figura recíproca de la de F1, 1 i 2 (fig. 31) amb la força F1 aplicada en el nus que formen a l’estructura les barres 1 i 2. Continuem traçant forces (de qualsevol magnitud i direcció) a partir de la F1 seguint l’ordre imposat per les paral·leles a l’estructura original 1…6 i de forma que el final de l’última força F6 coincideix amb l’origen de F1. D’aquesta manera, tindrem un polígon tancat de forces (qualssevol) en equilibri.

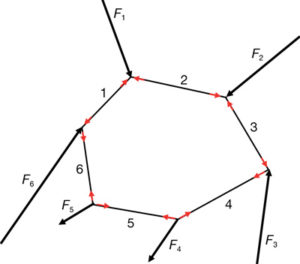
La intensitat i el signe de les forces que actuen en les barres de l’estructura queden definits per les distàncies entre el punt O i la magnitud de les línies 1…6, a escala de forces (fig. 33), i per l’inevitable equilibri que es dona entre els nusos (fig. 32). Observi’s que l’equilibri es dona per a qualsevol combinació de les forces F1…F6 amb l’única condició que formin un polígon tancat i respectin l’ordre imposat pel polígon recíproc a l’estructura.

MAXWELL

James Clerk Maxwell va néixer a Edimburg el 1831 i va morir a Cambridge el 1879. Va ser matemàtic i físic teòric. També catedràtic de Física i Astronomia a la King’s College de Londres i de Física Experimental a la Universitat de Cambridge. Tota la seva vida està impregnada d’una profunda fe religiosa. La fita més important de la seva recerca teòrica es troba a les 20 equacions diferencials ‘Equacions de Maxwell’ on d’alguna manera unifica les lleis bàsiques del magnetisme i l’electricitat amb la llum i determina les línies mestres de la ‘Teoria de la Relativitat’ d’Einstein i de mecànica quàntica.

Per cert, Einstein deia que Maxwell va fer l’aportació a la física més important des de Newton. Però a part d’aquesta recerca, Maxwell investiga la teoria cinètica dels gasos, la termodinàmica, les qüestions electròniques, l’equilibri dels sòlids elàstics, la percepció del color i la geometria pura. I encara li va quedar temps per estudiar la filosofia natural, la filosofia moral i la filosofia de la ment. Sense oblidar la passió que sentia pel dibuix i la geometria. Igual que Rankine, però amb no tanta intensitat, també canta i toca la guitarra. Igualment, compon poemes que van ser publicats. El seu poema ‘El cos rígid canta’ és un dels més famosos.

Com s’ha pogut comprovar a les línies precedents, la aportació de Maxwell a l’estàtica és totalment marginal en comparació a les altres matèries tractades. I en comparació amb Rankine i Cremona, és el més teòric i analític dels tres.

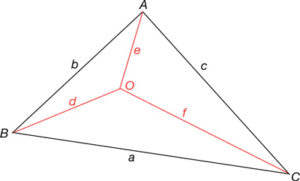
Tenim una estructura situada en un pla, de nusos articulats, composta per sis barres rectes i sense pes propi a…e, formada per quatre triangles i quatre nusos O-A…D i dibuixada a una certa escala de longituds.

Suposem que està en equilibri. L’estructura està sol·licitada exteriorment per forces al llarg de les barres d, e i f i aplicades en els nusos A, B i C encara sense definir els seus valors (fig. 34).

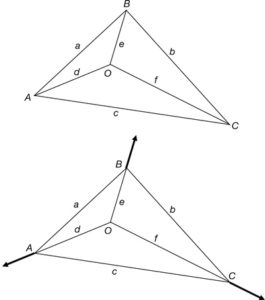
La figura recíproca a l’estructura és la que es dibuixa a continuació (fig. 35). Amb el mateix nom, però en color vermell, es designen les paral·leles a l’estructura original. En aquesta figura recíproca se li dona forma de polígon de forces, és a dir, que a cada barra se li associa una força en la qual encara no queda definida ni la seva intensitat ni el seu sentit. Precisament, aquesta definició és l’objectiu de la construcció que s’exposarà tot seguit.

De les tres forces que actuen en els nusos exteriors, considerem primerament la força de valor Ff segons la barra f aplicada en el nus C i dibuixada a una certa escala de forces (fig. 36). També podríem haver començat per qualsevol de les forces aplicades a les barres d o e.

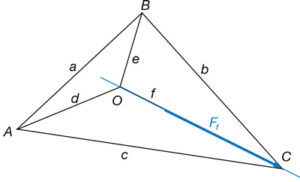
Es tracta primerament de trobar l’equilibri en el nus O de les tres forces sol·licitants.

La força aplicada en el punt O per la barra f té el valor Ff però en sentit contrari que l’aplicada en el punt C, ja que la barra f com a tal ha d’estar també en equilibri.

Col·loquem-nos a la figura recíproca ubicant, a escala de forces, el valor de Ff (fig. 37). Observi’s que el triangle d, e i f té unes dimensions en correspondència al valor de Ff. La figura recíproca ens donarà el valor de Fd i Ff (fig. 38).

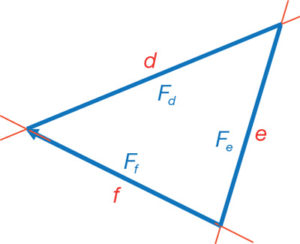
Ja s’ha creat la primera reciprocitat entre el nus O de trobada geomètrica de les tres barres d, e i f i les forces Fd, Fe i Ff que formen un triangle tancat en el polígon de les forces. Coneixem la intensitat de les forces, però ens fa falta el seu sentit.

Tot i que, en aquest cas, sigui molt simple observar el sentit de les forces perquè es doni l’equilibri, Maxwell dona un criteri molt senzill i fàcilment aplicable. Consisteix en col·locar un punt a la línia f i fer-lo córrer a través del polígon, en aquest cas un triangle, amb el sentit donat per Ff tal com s’indica a la figura, aconseguint el sentit de les forces Fd i Fe (fig. 39).

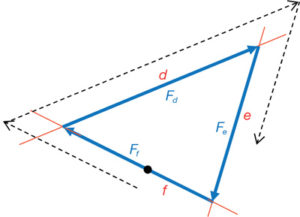
Fins ara, hem prestat atenció a la barra f en el seu extrem O de l’estructura. Analitzem ara l’altre extrem de la barra f, que té la seva representació recíproca en el triangle c, b i f. Si la força Ff és coneguda, el triangle ens donarà els valors de Fc i Fb segons les barres c i b.

Per tant, una vegada aconseguit l’equilibri en el nus O, la figura recíproca expressada en el seu polígon de forces ens ha donat l’equilibri en el nus C (fig. 40).

De la mateixa manera, obtenim l’equilibri en el nus B i l’A utilitzant els triangles a, b i e i el a, d i c respectivament de les figures recíproques. Tal com es veu a les figures 41 (nus B) i 42 (nus A).

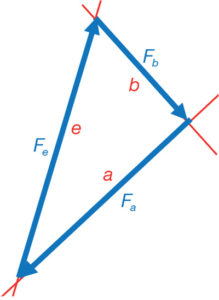
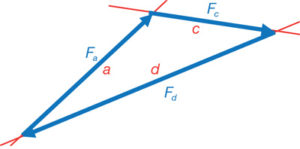
D’aquesta manera, l’estructura queda resolta. Tots els nusos de l’estructura estan en equilibri i, per tant, també la pròpia estructura en el seu conjunt. Es coneixen les forces que actuen en cadascuna de les barres i el seu sentit. El polígon de forces, com a recíproc de l’estructura original, ens ha donat aquests valors de forma automàtica. Observi’s que, en cap moment, s’ha utilitzat el mètode del paral·lelogram.

Traslladant els sentits de les forces del polígon de forces a l’estructura original tindrem el següent esquema, on les barres a, b i c es troben traccionades i les d, e i f comprimides (fig. 43). Una forma intuïtiva de conèixer el sentit de les forces és suposar que l’estructura és la projecció horitzontal d’un poliedre de base A, B i C i vèrtex O elevat amb referència al pla horitzontal. Si considerem el vèrtex O inicialment en el pla horitzontal i intentem elevar-lo, ens trobarem amb les barres que conflueixen al punt O comprimides i les del pla horitzontal traccionades.

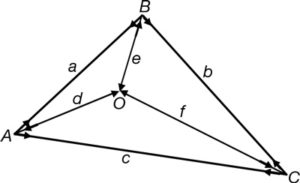
Hem estudiat el que passa als voltants de la barra f i com els punts d’intersecció de barres en els nusos O i C s’han convertit per reciprocitat en els triangles de forces Ff , Fd i Fe i Ff, Fb i Fc.

Observem, a continuació, la mateixa barra f com un costat comú als triangles AOC i BOC.

Per la pròpia definició de reciprocitat, el recíproc de la figura AOBCA (inclosa la barra OC) no és un punt, i per tant, les forces que transiten per aquesta figura no estan en equilibri (fig. 44).

D’aquesta manera, per exemple, el costat c en el polígon de forces, s’haurà de dibuixar a partir de les paral·leles a les barres f i d i no a partir de les a i b. D’igual manera passa amb la construcció de les línies a i b del polígon de les forces. En tot cas, com es veu a la figura 45, no pot ser que dos triangles diferents tinguin la mateixa figura recíproca.

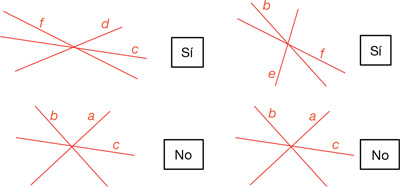
Estem ara en condicions d’exposar el següent teorema geomètric de Maxwell, que donarà com a vàlides les condicions de reciprocitat exposades fins ara. Seguint el mateix esquema de figures: si les barres a, b i c partint dels nusos A, B i C es troben en un punt O, i d, e i f formen un triangle construït a base de traçar paral·leles a les barres d, e i f, aleshores les línies a, b i c del polígon de forces es trobaran també en un punt (figures 34 i 35).

En efecte³, trobem els cercles circumscrits dels triangles ABO, BCO, ACO i ABC, aconseguits a base de traçar mitjanes als costats corresponents, i sobre elles trobarem els circumcentres dels cercles circumscrits de posició O, O, O i O (fig. 46).
³ És condició suficient per demostrar un teorema d’un context gràfic o geomètric comprovar que, efectivament, el teorema té recíproc o, en altres paraules, si un teorema té recíproc no cal demostrar-lo.

Si unim amb rectes els centres dels cercles, obtindrem les línies m, n, o, p, q i r (fig. 47).

Cadascuna d’aquestes línies són perpendiculars a la de l’estructura original. Les línies m, n, o, p, q i r són, per tant, perpendiculars respectivament a e, f, d, a, b i c. Les línies creades a partir dels circumcentres han resultat perpendiculars a les línies de l’estructura original. Si les girem 90 graus, les línies de la figura resultant són paral·leles a l’estructura original (fig. 48).

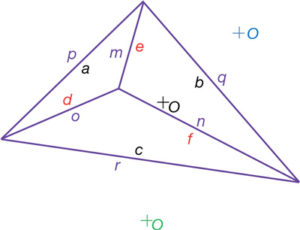
I es dona, a més, que les línies m, n i o es troben en un punt. A més, la figura obtinguda és idèntica a la figura original però recíproca de la que uneix els circumcentres.

CREMONA

Antonio Luigi Gaudencio Giusepe Cremona neix a Pavia el 1830 i mor a Roma el 1903. Matemàtic. Degut al seu neguit nacionalista va combatre a la guerra contra l’exercit austríac. Quan va acabar la guerra, les institucions dominades pels austríacs li van posar obstacles, per exemple, per entrar de docent a la universitat, cosa que va determinar que el seu inici a la vida acadèmica i de recerca es retardés fins als trenta anys.

Obté el doctorat amb una tesis sobre mecànica clàssica. Catedràtic de geometria superior a la Universitat de Bolonya i professor al Politècnic de Milà. Dirigeix l’escola d’enginyers de la Universitat de Roma. Va introduir l’estàtica gràfica i la geometria projectiva (és una branca de la matemàtica) a leS escoles secundàries i superiors italianes. Estudia les transformacions de corbes i superfícies tridimensionals i fa moltes publicacions, especialment tractats de geometria. El seu prestigi arriba a Europa i el fan membre de la Royal Society de Londres. El 1879 és nomenat senador i deixa l’activitat acadèmica. És per això que la dedicació a la recerca de Cremona és relativament curta.

Dels tres investigadors que tractem en aquest estudi, Cremona és l’únic que té un llibre dedicat exclusivament a les figures recíproques Le figure reciproche nella Statica Grafica, llibre que tindria una influència molt significativa a les posteriors promocions d’enginyers.

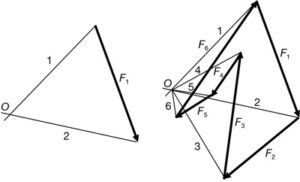
Disposem de l’estructura plana composta de barres 1…6 i nusos articulats sol·licitada per un conjunt de forces F1…F6 amb unes línies d’acció que es troben en el punt O (fig. 49).

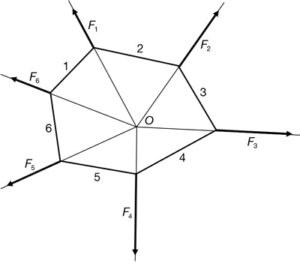
Si l’estructura es troba en equilibri, les paral·leles a les forces col·locades correlativament han de formar un polígon tancat (fig. 50).

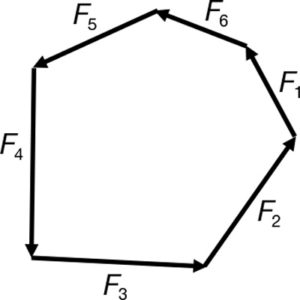
Si des d’un punt qualsevol interior (o exterior) al polígon de forces O tracem línies a l’origen i final de totes les forces 1…6 (fig. 51) i aquestes línies les traslladem a l’estructura, tindrem el polígon tancat 1…6 (fig. 52).

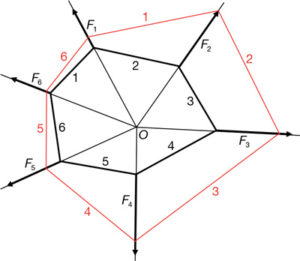
D’aquestes construccions es pot dir: les dues figures formades són recíproques o bé, donant-li un aspecte espacial com indicava Cremona, les projeccions ortogràfiques dels dos poliedres de vèrtexs O i O són recíproques.

Per exemple, el triangle 1-6-F1 del polígon de forces (fig. 51) té la seva correspondència recíproca a l’estructura amb la coincidència que formen les línies 1-6-F1 (fig. 52), i al mateix passa amb les diferents línies de les dues construccions.

Generalitzarem la mateixa estructura anterior de la figura 49 amb forces F1…F6 que no es troben en un punt (fig. 53).

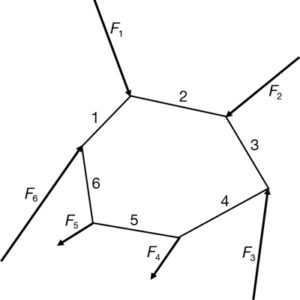
L’estructura està sol·licitada per un conjunt de forces F1…F6 que no coincideixen en un punt però que, tal com es veu a la figura 54, estan en equilibri ja que les seves paral·leles col·locades per ordre i, una a continuació de l’altra, formen una figura tancada.

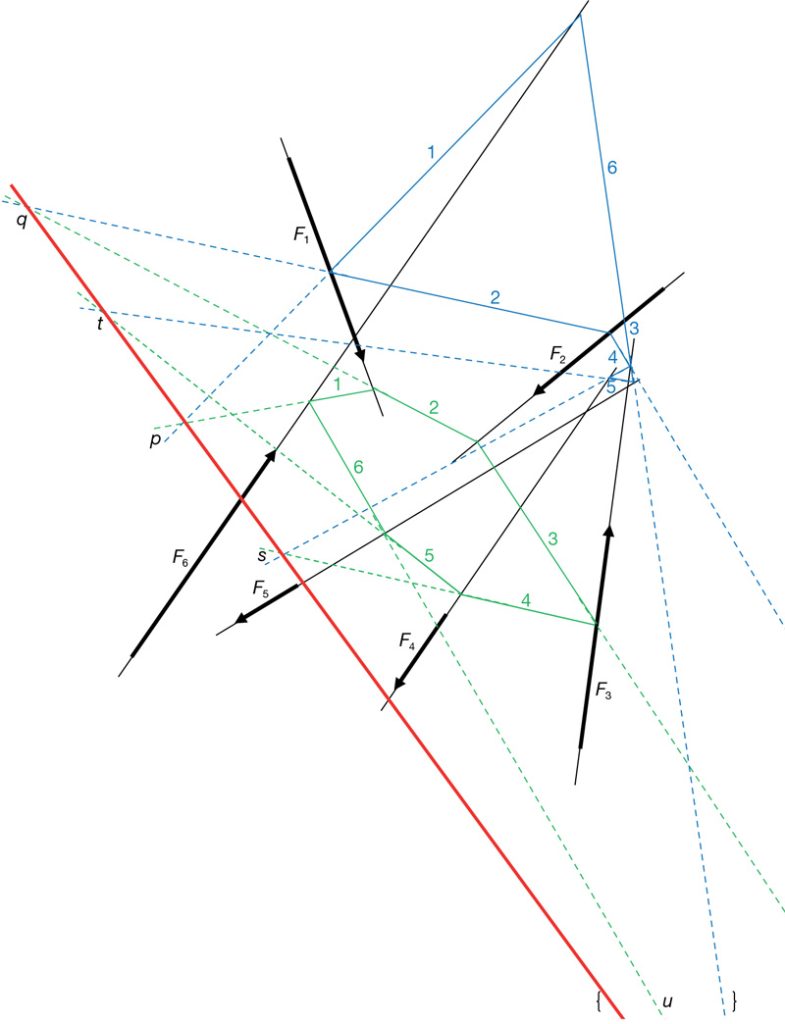
Des d’aquest conjunt de forces en equilibri marquem dos punts o pols O i O qualssevol i des d’aquests tracem línies 1…6 i 1…6 als extrems de les forces. Des de dos punts qualssevol de les forces de l’estructura tracem paral·leles consecutives, tal com es veu a la figura 55, obtenint les figures tancades 1…6 i 1…6. Això és així perquè les forces es troben en equilibri. La prolongació de les línies del mateix número de cada figura ens donen uns punts de coincidència que anem nomenant com p a la trobada de les línies 1 i 1 i, finalment, u a la trobada de 6 i 6, tot i que alguns d’aquests punts es fan no visibles per disponibilitat del paper. D’aquesta construcció de Cremona es fan les següents consideracions.

1. A la figura 54 es representa la projecció ortogràfica de dos poliedres de vèrtexs O i O, respectivament, i que es representen en l’espai a la figura 56. Es vol fer palesa la interrelació entre les dues i tres dimensions. A més, la línia O-O per on corren els vèrtexs dels poliedres és la conjugada de la línia q…u.
2. Les línies 1…6, arestes del poliedre i que es troben en el vèrtex O de la figura 54, són recíproques de les paral·leles a aquesta en la figura 55 i formen una  figura tancada. De la mateixa manera passa amb les línies 1…6 de vèrtex O.
3. La línia que uneix els dos pols O i O de la figura 54 és paral·lela a la línia q…u de la figura 55.
4. La línia q…u és allò que es coneixeria com ‘Eix de Culmann’. És el lloc geomètric de les interseccions dels costats dels polígons funiculars, en els quals els pols es mouen segons la línia O-O. Culmann utilitzaria aquesta propietat com, per exemple, entre altres coses, per fer passar un polígon funicular per tres punts. Però Cremona dona a aquesta línia simplement un valor recíproc, és a dir, per exemple, les línies 1, 1 i q…u de la figura 55 coincideixen en el punt p, mentre que les línies 1, 1 i O-O de la figura 54 formen un triangle. I el mateix es pot dir de les altres línies construïdes entre les figures 54 i 55.
5. Per conèixer els esforços a què estan sotmeses les barres de l’estructura s’ha de realitzar un altre exercici de reciprocitat. A qualsevol força, per exemple la F1, observem el nus on actua i la vinculació amb les barres 1 i 2. Si tracem les paral·leles a F1 i a les barres 1 i 2 des de l’extrem de F1 tindrem definit el pol O que ens subministra les forces a què estan subjectes les barres (fig. 57). Quan des d’aquest pol tracem les altres línies a les forces col·locades una darrera de l’altra per ordre, aquestes línies definiran, a escala de forces, les sol·licitacions a les quals cadascuna de les barres està subjecta.
   La figura 58 indica simplement el signe de les sol·licitacions
   a les diferents barres.

La sublimació de l’estàtica reciprocista es troba en el ‘Mètode de Cremona’ per a la resolució d’estructures isostàtiques en el pla, compostes per barres i amb els nusos articulats. La gran quantitat de barres de què poden estar compostes aquestes estructures les fa complexes. Cremona, basat en la superposició de figures recíproques, resol el problema de forma relativament simple. Observem el següent exemple, extret de la figura 7 de la planxa que es troba al final del llibre Le figure reciproche nella Statica Grafica (fig. 59).

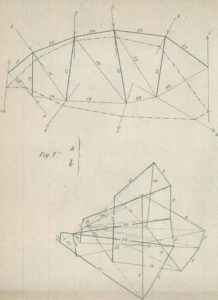
Cremona explica en poques línies el funcionament d’aquesta estructura basat en el seu propi mètode. Intentarem esbrinar el fort contingut reciprocista d’aquest exemple.

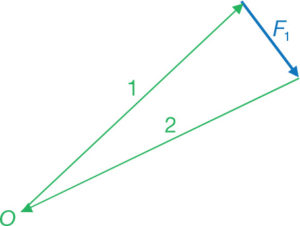
Suposem una sèrie de forces F1 a F10 qualssevol amb línies d’acció no coincidents i situades en un pla (fig. 60).

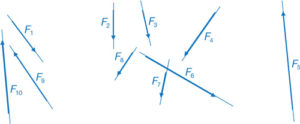
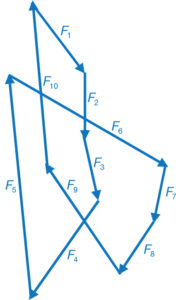
L’única condició, però la més significativa, és que s’obliga a què aquestes forces estiguin en equilibri, tal com s’observa en la figura 61, on efectivament les paral·leles a les forces col·locades correlativament al final de la força F10 coincideixen amb l’origen de la força F1.

Des d’un punt o pol qualsevol O, tracem línies a l’origen i al final de les forces, obtenint les línies 1…11 (fig. 62). Traçant paral·leles a aquestes línies en el sistema de forces obtenim el diagrama tancat de la figura 63.

D’aquests diagrames s’extreuen les següents conclusions:

1. Les figures dibuixades en color verd dels dos diagrames són recíproques.
2. Els radis de la figura 62, polígon de forces, expressen forces. Per exemple, el triangle format per F1, 1 i 2 indica que les forces que transiten per les línies 1 i 2 equilibren la força F1.
3. Observem del mateix polígon els triangles formats per F1, 1 i 2 i F2, 2 i 3. La força generada a la línia 2 de la figura 64 és anul·lada per la força generada a la mateixa línia de la figura 65.

Per tant, la forma obtinguda a la figura 63 (una de les infinites que es poden tenir en funció de la posició del punt O) no té res més que un significat geomètric. Per dir-ho en altres paraules, una forma similar a l’obtinguda podria ser una estructura composta per barres en el pla. Per aquestes barres circularien forces amb uns certs valors que les comprimirien o traccionarien. Amb aquests esforços i triant un material, es podrien dimensionar estructures, de tal manera, que fossin estables i amb suficient seguretat.

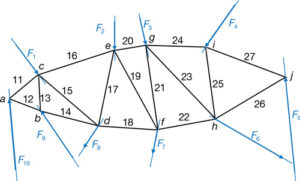
Cremona proposa el següent esquema, que recorda la disposició de la figura 63 (una cosa semblant a una encavallada) sol·licitada per les mateixes forces de la figura 60 (fig. 66). Es tracta d’una estructura isostàtica⁴ en el mateix pla que el de les forces. Composta per 17 barres 11…27 i 10 nusos a…j. Articulada, de tal manera, que en les barres no es pot generar altra cosa que compressions o traccions.

⁴Perquè una estructura composta de barres sigui isostàtica, s’ha de complir la següent relació: 2 · n 2 b 5 3. Sent n el nombre de nusos i b el nombre de barres. En el nostre cas és n 5 10 i b 5 17, que compleix la relació.

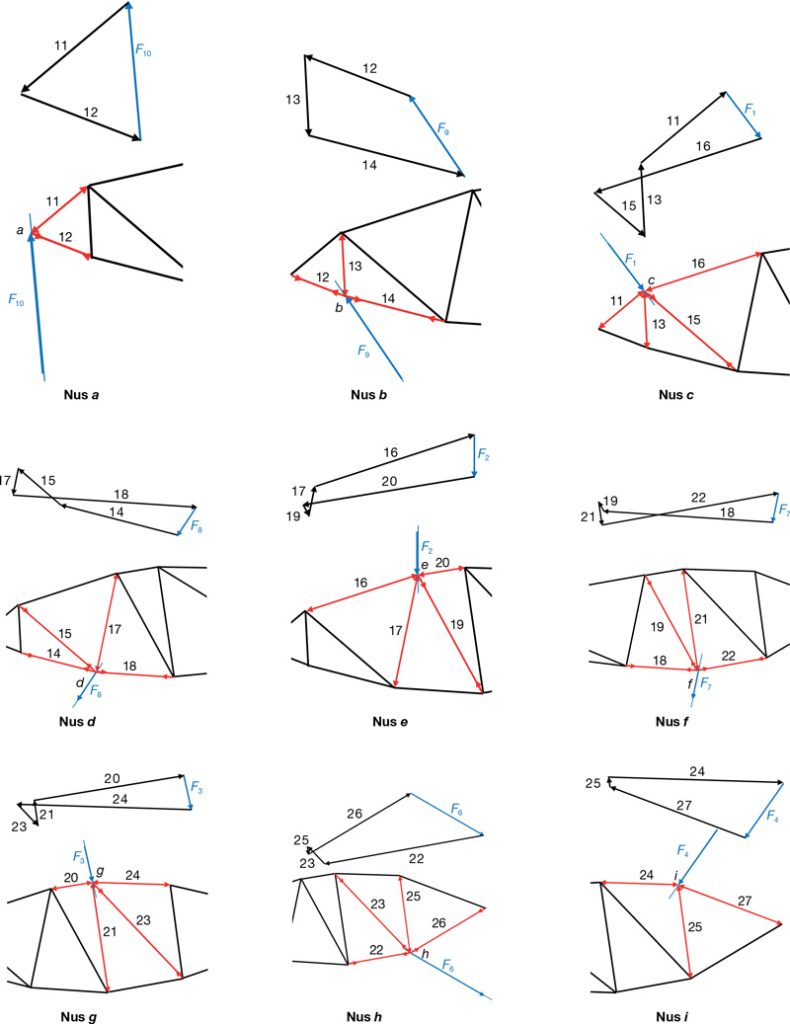
Sobre aquesta estructura, Cremona aplica el seu mètode per trobar les sol·licitacions a què es troben subjectes les barres (fig. 67) i podem indicar les següents qüestions:

1. A cadascun dels nusos de l’estructura es dona la reciprocitat en el diagrama de Cremona. Per exemple, en el nus c les barres 11-13-15-16 i F1 formen una figura tancada en el diagrama de Cremona.
2. Cremona avança en el sentit que es cregui més oportú, però de forma que les incògnites en cada nus no siguin més que dos. En el nostre cas, avancem en l’ordre alfabètic indicat en els nusos.
3. Una vegada resolt un nus en el diagrama, s’avança, de tal manera que les línies del diagrama se superposen. Aquesta és la propietat fonamental del ‘Mètode de Cremona’. Per exemple, la barra 12 del nus a és també la barra 12 del nus b.
4. L’esforç a cadascuna de les barres ve determinat al diagrama de Cremona mesurant les longituds de les línies a escala de forces.
5. Cremona exposa un criteri per a la determinació dels signes una mica complicat. Maxwell, que no es tan didàctic com Cremona, exposa, no obstant, el seu criteri de signes de forma més fàcil i intuïtiva, com es comprova a la figura 39. Maxwell, com s’ha vist, va estudiar les figures recíproques potser amb més intensitat que Cremona, però es deu a aquest l’operativitat del mètode. Per això, es diu a vegades el ‘Mètode de Cremona-Maxwell’.
6. A la figura 68 es dona la reciprocitat en tots els nusos (excepte el nus j, on el seu equilibri ve donat pels seus nusos veïns) que formen l’estructura.

CONCLUSIÓ

Les teories reciprocistes han donat dos fruits que es consideren de gran importància en el càlcul estructural. D’una banda, el polígon funicular, que permetrà traçar, en primer lloc, les línies de pressió dels arcs, però també d’ajuda a allò que podríem anomenar l’estàtica elemental: centres de gravetat, moment de inèrcia, etc., sense oblidar les aplicacions en el formigó armat, escalars, etc. D’altra banda, el mètode de Cremona per al càlcul d’estructures de barres isostàtiques en el pla ha estat ensenyat a generacions d’enginyers i el servei prestat ha estat immens.

BIBLIOGRAFIA

Rankine

A la pàgina 137 del llibre Manual of applied Mechanic (1858, Charles Griffin & Company) Rankine estudia les figures recíproques aplicades al polígon funicular quan a aquest encara no se li havia donat l’alçada intellectual proclamada per Culmann. Existeix una traducció al francès del mateix llibre, Manuel de Méchanique Applieé (1876, Dunot Editeur, Paris). Els dos llibres, gairebé complets, poden consultar-se per internet.

En el Philosophical Magazine de febrer de 1864 Rankine anuncia aspectes de la reciprocitat de figures en l’espai.

També es poden consultar qüestions relacionades amb la reciprocitat a Frames of roofs de 1872 en el volum 33 de la publicació The Engineer.

Maxwell

Les consideracions de Maxwell sobre reciprocitat no es troben editades en cap llibre. Només es coneix un article publicat en el volum XXVI de ‘Transactions of the Royal Societe of Edinburgh’ el 1870 titulat On Reciprocal Figures, Frames, and Diagrams of Forces.

En el Philosophical Magazine d’abril de 1864 i a la British Association de setembre de 1867, Maxwell torna a la càrrega sobre mètodes per dibuixar figures recíproques a partir de la teoria dels polars recíprocs. També estudia la reciprocitat en l’espai.

Cremona

Cremona escriu llibres sobre matemàtiques i geometria projectiva però, on s’exposa el contingut de les figures recíproques, és a Le figure reciproche nella Statica Grafica (Milà, 1885). També existeix una traducció a l’anglès de Thomas Hudson Beare de 1890 Graphical statics. Two treatises on the graphical calculus and reciprocal figures in graphical statics.

Altres publicacions o llibres consultats són els següents:

• La Estática Gráfica instrumento para el conocimiento estructural intuitivo y el diseño de los arquitectos. Juan Gómez Acosta. Universitat Politècnica de València. 2013.
• Polígon funicular. Una aproximació a Karl Culmann. Josep M. Genescà Ramon. IEE Institut d’Estudis Estructurals. Barcelona, 2018.