L’ÚS DE LA VOLTA CERÀMICA PER CONTENCIÓ DE TERRES. UNA SOLUCIÓ MOLT SOSTENIBLE

ROBERT BRUFAU I NIUBÓ (Mollerussa, 1946)

Doctor Arquitecte; President de la Fundació Privada Institut d’Estudis Estructurals (IEE); ha sigut President de l’Associació de Consultors d’Estructures (ACE) de 1987-1995.
Professor Titular del Departament de Tecnologia en l’Arquitectura de la UPC, Àmbit d’Estructures.
Soci Fundador de BOMA, S.L.; Soci Fundador de BBG estructures, recerca i rehabilitació, S.L.P.

Aquesta conferència la vaig pronunciar, el mes d’octubre del 2022, a la fàbrica ASLAND, a l’obra que Guastavino va construir a Castellar de n’Hug. Eren les IV Jornades Tècniques, que amb un interval de dos anys es realitzen en aquest marc. Aquesta vegada, el tema va ser: «La volta catalana: arquitectura sostenible».

Començo explicant uns conceptes bàsics per entendre el que exposaré en aquesta sessió.

Treballar per la forma

És una de les maneres més sostenibles per fer arquitectura, ja que és minimitza la quantitat de material a emprar. Es basa en el treball pur dels elements a esforços axials de tracció o de compressió, minimitzant el treball a esforços flectors i tallants.

Les catenàries i els polígons funiculars. La seva inversió

Es tracta d’un mètode per aconseguir esforços axials purs de compressió. Si nosaltres suspenem una cadena formada per un seguit de petits anells consecutius, només hi haurà una forma possible. És la que disposaria cada petita peça de manera que s’encadenessin esforços axials purs de tracció entre elles.
La cadena no pot treballar a compressió, perquè pandejaria, ni a tallant, ni a flexió, ni a torsió, perquè perdria la forma. Igual que un cable, una cadena despenjada únicament pot quedar sol·licitada per traccions.
Si la veiem amb un mirall horitzontal que la reflecteix, veurem la forma invertida, i l’esforç axial de tracció es convertirà en esforç axial pur de compressió, sense que hi hagi excentricitats de la resultant respecte a l’eix de la peça. I si no hi ha excentricitats, no hi hauran ni flectors ni tallants, i el pandeig es manifestarà molt difícilment.
A la imatge superior dreta de la figura 1 hi podem veure l’experiència d’una inversió catenàrica, fixant els dos punts extrems amb els dits i deixant que la cadena agafa l’única forma bona per treballar a esforç axial pur. A l’invertir-la, tindrem la forma de compressió pura. Veiem a la imatge superior esquerra de la figura 1 la silueta d’un pont japonès construït amb aquest criteri: el reflex a l’aigua coincideix exactament amb la cadena que subjecten les dues mans.
Les imatges inferiors del costat esquerra de la figura 1 en són un bon exemple. A l’altiplà bolivià, una forma curiosa de construir és la que despenja una cadena amb la mateixa longitud en planta que tindrà la construcció que es vol fer. Mesurant les distàncies des de la línia horitzontal que marquen els claus superiors fins a la cadena deformada, poden obtenir la geometria de la forma i el patró de la construcció optimitzada. Van posant els totxos lleugerament inclinats per evitar-se el cindri d’encofrat i així poden acabar tancant la preciosa construcció que es veu a la imatge de la dreta.

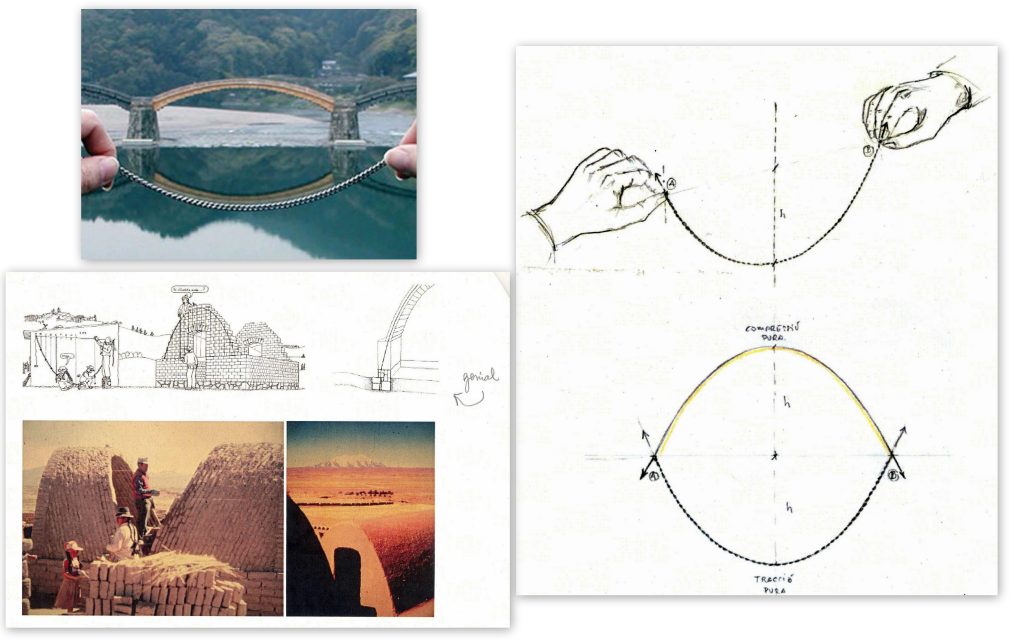
Figura 1.

La construcció catalana està plena d’exemples en aquesta línia. Els principals mestres del modernisme, per exemple, van dominar a la perfecció aquesta tècnica. Les obres que es mostren corresponen a un celler vitivinícola de César Martinell, on es pot veure la solució murària invertida, amb els arcs molt optimitzats (fig. 2). També Gaudí i els seus deixebles dominaren aquesta tècnica, bàsicament pel seu domini de l’estàtica gràfica, una manera d’entendre el treball resistent que va quedar bastant eclipsada amb l’aparició dels programes de càlcul per ordinador (fig. 3). Soc dels que penso que ens faria molt de bé recuperar-la.

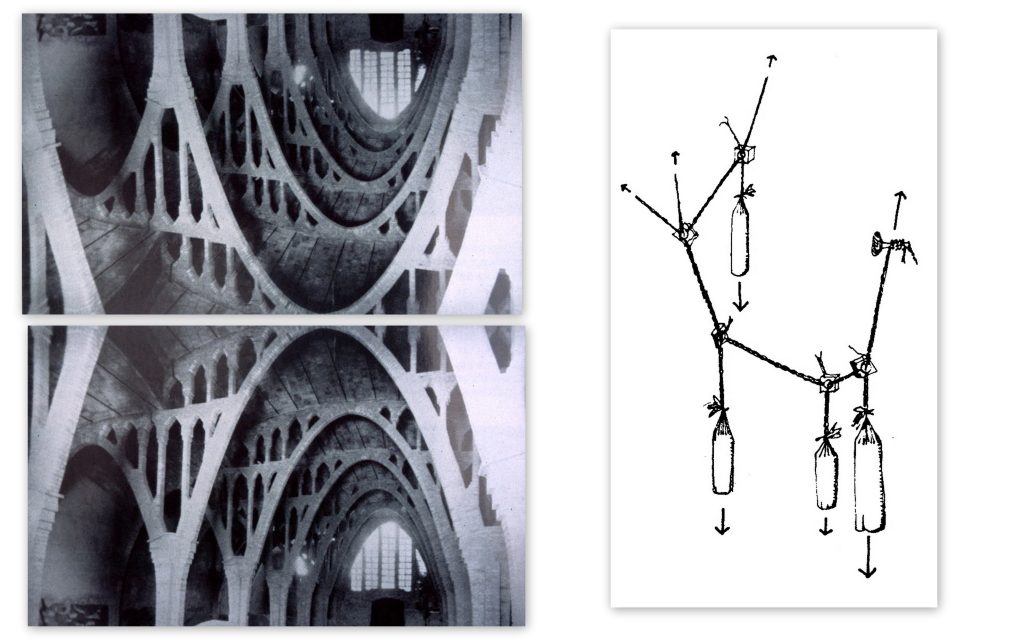
Figura 2.

Figura 3.

La figura 4 ens mostra dues inversions funiculars del món gaudinià, Ja no es tracta només d’invertir una cadena, sinó que la solució s’estén a estructures tridimensionals amb una forta component espacial. Podríem dir que les inversions no tenen límit quan es tracta de materialitzar estructures complexes o de gran extensió

Figura 4.

És, precisament, el que va fer Frei Otto quan va projectar la Sala Polivalent de Mannheim a partir d’un model invertit, com es veu a la figura 5, on també, al dibuix central, si torna a veure una de les experiències gaudinianes.

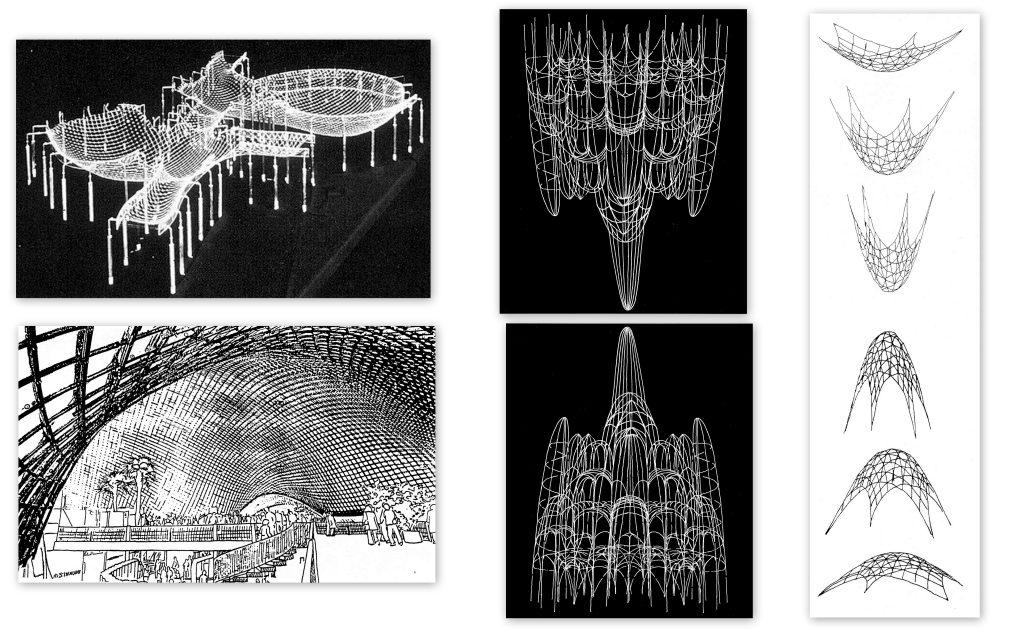
Figura 5.

L’obra de l’enginyer Sánchez del Rio: Un precedent interessant

L’enginyer asturià Ildefonso Sànchez del Rio (1898-1980) fou un gran entusiasta de l’estàtica gràfica, que va estar present ja des de les seves primeres obres, l’any 1925. Les catenàries (en posició, o invertides), i també els funiculars, els va fer servir abastament a tota la seva obra ¹.

Figura 6.

Mostrem l’insòlit Palau d’Esports d’Oviedo, amb una llum de 100 metres. És una veritable joia de l’enginyeria espanyola, ja que fou construïda amb dovelles i arcs ceràmics. L’armadura de reforç era relativament poca i la disposava únicament per controlar les accions eòliques. A les figures 7 i 8 hi veiem la inversió catenàrica de la gran nau, tant pel que fa als arcs principals com a les dovelles-arc.

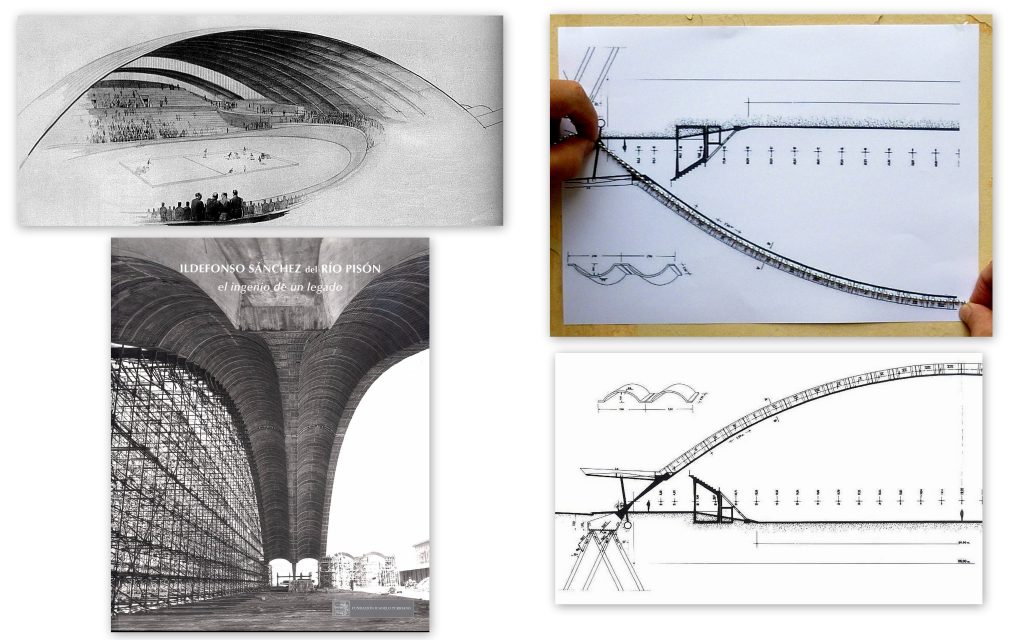
Figura 7.

Figura 8.

¹ La catenària la va emprar Ildefonso, sense invertir-la, en una de les obres més agosarades que mai s’han construït. És una peça única, que vaig tenir la sort de rehabilitar ara farà uns cinc anys. Es tracta del “Paraigües del Bestià” (fig.6), construït per aixoplugar el bestià els dies de Mercat, a Pola de Siero (Astúries). Es tracta d’una peça circular en planta, de 40 metres de diàmetre, amb vuit grills radials i amb un únic pilar central de només 90 cm. de diàmetre. Però el mostro aquí, no per l’audàcia general del projecte, sinó per les impressionants catenàries, amb un gruix de només 4 cm. per cobrir una separació de més de 15 metres entre nervis, al perímetre exterior. Aquestes catenàries són de formigó armat i treballen a tracció pura degut a la precisió de la seva forma. La rehabilitació de l’any 2017 va ser per recuperar la qualitat del material, bastant degradada per culpa dels baixos recobriments de l’armadura.

He mostrat aquestes estructures perquè tenen bastant a veure amb els tipus estructurals que Ildefonso va emprar per fer grans dipòsits, per tota Espanya (a Terrassa hi té l’imponent Dipòsit d’aigües de la Mola, recentment rehabilitat), per contenir grans volums d’aigua.

Comencem veient el Dipòsit d’Oviedo (1927) una singular construcció radial en la que, per contenir l’aigua emmagatzemada, utilitza voltes amb forma de catenària invertida, suportades pels 48 arcs, a la manera del que uns anys més tard construirà al Palau d’Esports d’Oviedo. Al perímetre exterior, de prop de 200 metres de longitud corba, hi va disposar 48 contraforts de pedra, amb alçat trapezoidal, que, a més de rebre els arcs de la coberta, servien per suportar les catenàries verticals que s’enfrontaven a l’empenta de l’aigua, lliurant-se en els contraforts immediats pels dos costats.

Sánchez del Río va emprar diferents materials pels seus dipòsits: en algunes ocasions va fer ús de la ceràmica per tots els elements, però tampoc són rars els dipòsits que va fer, amb el mateix criteri organitzatiu, amb formigó armat. Els contraforts eren molt sovint petris, amb mamposteria amorterada, treballant a compressió gràcies a la geometria del seu alçat. Curiosament, es pot veure com el dipòsit va resistir un fort atac bèl·lic, durant la Guerra Civil (fig.9).

Figura 9.

Al següent dipòsit, bastant més petit, que va construir a Pola de Siero, s’hi pot observar un aspecte curiós. En efecte, el dipòsit està semisoterrat, i a la secció hi veiem que mentre les terres afecten directament el perímetre, aproximadament a la meitat de la seva alçaria, les voltes estan reforçades, amb un gruix molt major, i probablement amb formigó adequadament armat, mentre que els contraforts segueixen sent petris. A la figura 10, la fotografia general de l’interior s’hi pot observar que tot estaria preparat per que l’aigua pogués arribar fins al nivell de les finestres.

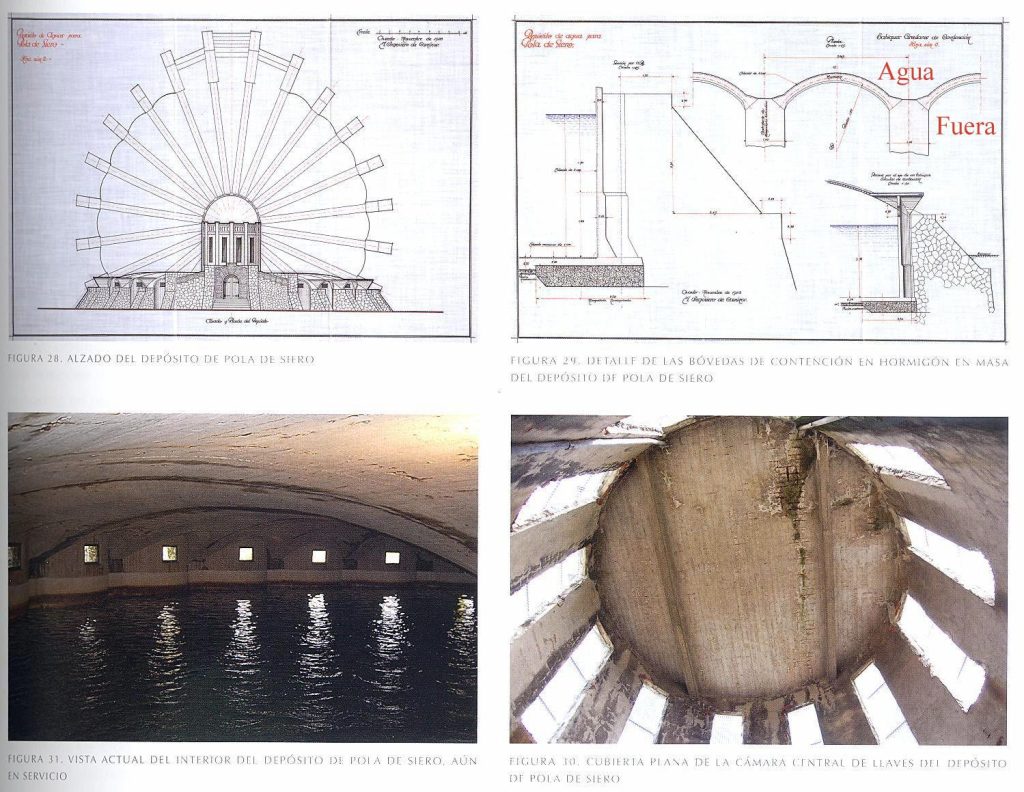
Figura 10.

Un curiós exemple d’enginy popular a les terres de Tarragona

L’any 1952 es va construir, al Mas de Sant Rafel, un força imponent dipòsit d’aigua, amb una altura que no estaria lluny dels 6 metres, projectat per un arquitecte no conegut. L’enginy que hi ha a la solució fa pensar que potser coneixia les obres de Sánchez del Río, però penso que va anar encara més lluny al fer les voltes amb paret de totxo (fig. 11, imatge superior dreta). Veient les fotografies de la figura 11, sembla que el dipòsit està ara fora de servei, però resta en el seu lloc amb un aspecte imponent.

Figura 11.

Les presses dels grans pantans, un bon exemple de geometria per contenir l’aigua

La geometria hiperbòlica que caracteritza les formes catenàriques és la que garanteix que aquests elements que, fins ara, hem vist aplicats per contenir aigua de dipòsits, tinguin la seguretat suficient. Anant del més petit al més gran, mostro ara una de les formes habituals per fer les presses de contenció dels pantans. Quan les muntanyes que els voregen tenen suficient capacitat resistent per rebre les immenses empentes que els hi arribaran, la solució funciona, i les fotografies de la figura 12 així ho posen de manifest.
L’esquema superior del costat esquerra de la figura 12 ho explica molt bé. La forma arquejada de la pressa empenyerà contra les dues muntanyes immediates i el sistema esdevindrà estable. El pes propi de la paret de la presa es transmetrà cap al terreny de base. La secció de la paret de la pressa serà més ampla com més prop estigui del terra, atès que els esforços creixeran sensiblement a mida que es vagi contenint una major altura d’aigua en el trasdós.

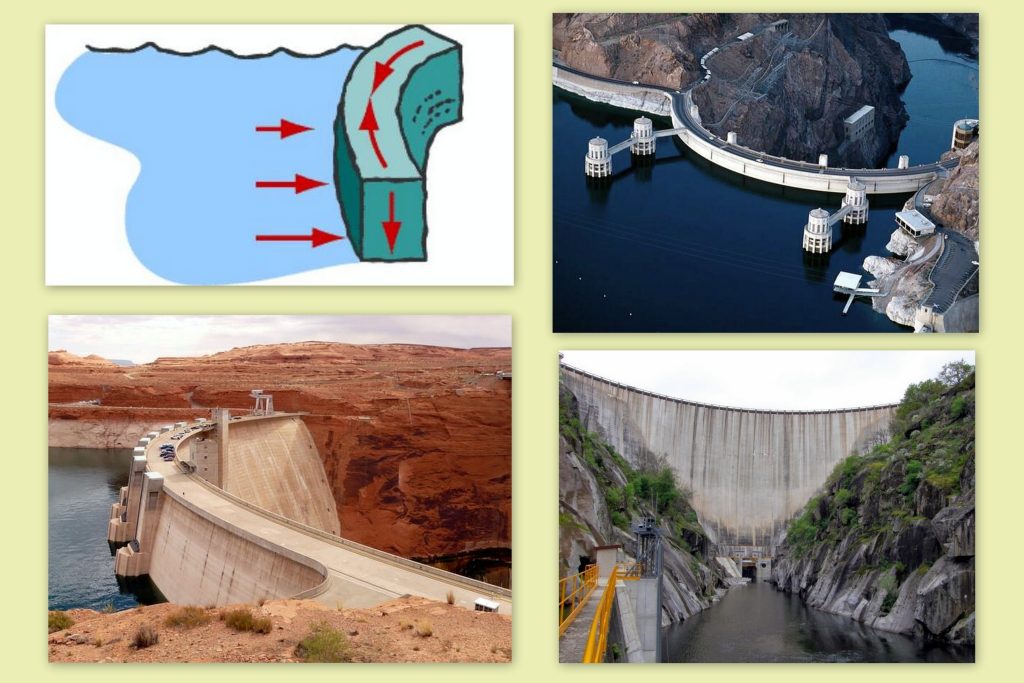
Figura 12.

Si es pot contenir aigua, perquè no es podrien contenir les terres en una edificació?

Les empentes de l’aigua tenen valor uniforme sobre la superfície que les suporta. La seva intensitat depèn de la fondària de l’aigua que suporta a cada nivell, seguint el principi de l’empenta hidrostàtica que produeix l’aigua en el mur contenidor.
L’empenta adopta la forma geomètrica triangular, amb un valor a la base, en t/m2, igual a l’altura de l’aigua continguda. Els moments flectors del mur vertical tenen el valor que es veu a la figura 13, si el mur es fa treballar a flexió.
Si en comptes de terra haguéssim de contenir terres, tot es reduiria sensiblement, sent bastant menors els valors de les empentes, així com els dels moments flectors màxims, que finalment serien els que imposarien l’amplada del mur.
Així, doncs, les empentes que produirien les terres contingudes serien força menors que les que produïen, per exemple, les aigües contingudes als dipòsits de Sánchez del Rio o al del Mas de San Rafel que hem vist abans.

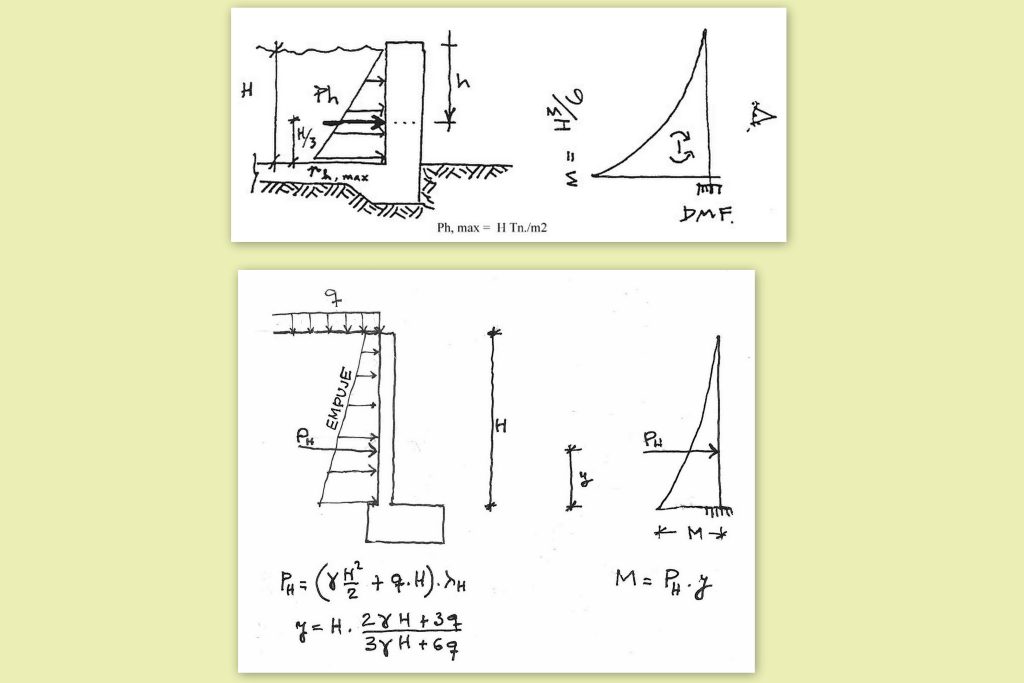
Figura 13.

I, si allà s’hi van utilitzar voltes de poc gruix, amb la geometria procedent d’una inversió catenàrica, perquè no pensar en utilitzar el mateix sistema per contenir terres a l’edificació ordinària, especialment quan el terreny sigui acceptablement uniforme i sense incidències localitzades de càrregues immediates (construccions altes, adossades en un tros del límit del solar, per exemple) que ho alterarien?
Tinguem en compte la importància que tindria treballar amb una “forma pura” que només mobilitzaria esforços axials, de compressió en aquest cas, defugint completament la presència de moments flectors i esforços tallants. El gruix d’aquests elements catenàrics seria bastant reduït i el consum de material disminuiria enormement, fent més sostenible el sistema constructiu emprat, si el comparem amb l’habitual manera de resoldre el problema, amb murs verticals de formigó armat, treballant a flexocompressió.

Una experiència viscuda fa prop de 40 anys: Les caves Raventós, a Sant Sadurní d’Anoia

Les caves de magatzematge d’una empresa del món del Cava que estava construint el seu nou edifici, amb els arquitectes G.Mora i J.Bach, tenia que resoldre l’estructura de contenció del terreny que embolicava la planta soterrada.
Estàvem en un territori on hi havia una forta tradició en la construcció artesanal ceràmica. En el moment d’iniciar el projecte se’ns va assabentar d’aquesta circumstància, i, tots plegats, pensàrem que podria ser una bona ocasió per experimentar amb nous sistemes de contenció. Tot el projecte era molt innovador, i l’estructura no podia ser menys. La cava s’ubicaria a la planta soterrada, i tindria una fondària propera als 6 metres, quedant rodejada pel terreny en gairebé tota la seva altura (fig,14).

Figura 14.

L’estructura que cobria aquesta cava inferior era a base de pòrtics de formigó armat, amb jàsseres de bastant cantell i pilars de planta sensiblement quadrada.
Com a sostre es van utilitzar voltes ceràmiques, amb geometria propera a la d’una catenària invertida (a l’aplicar la sobrecàrrega sobre un pla horitzontal, però, la geometria no era exactament catenàrica) formades per tres mans de totxo, de 5 cm de gruix cada una. Damunt seu s’aixecaven tabicons conillers que acabaven suportant un encadellat ceràmic i una llosa de rodadura de formigó armat, tot plegat preparat per sobrecàrregues d’ús de gran intensitat, de l’ordre, si no recordo malament, de 2000 Kg/m2, pel pas de camions per la planta superior (fig. 15).

Figura 15.

Ens resultava atractiva la idea de que les imponents bigues del sostre giressin verticalment a l’arribar al mur de contenció de dos dels quatre costats de la nau, convertint-se en els pilars. Però més interessant ens va semblar que també fos la volta catenàrica la que girés al arribar al mur, disposant-se verticalment entre els pilars, que farien ara també de contrafort per rebre les empentes de les terres, el que condicionaria l’existència de molta armadura i una geometria en planta força allargada, com correspon a la important tasca resistent que hauria de dur a terme (fig. 16).

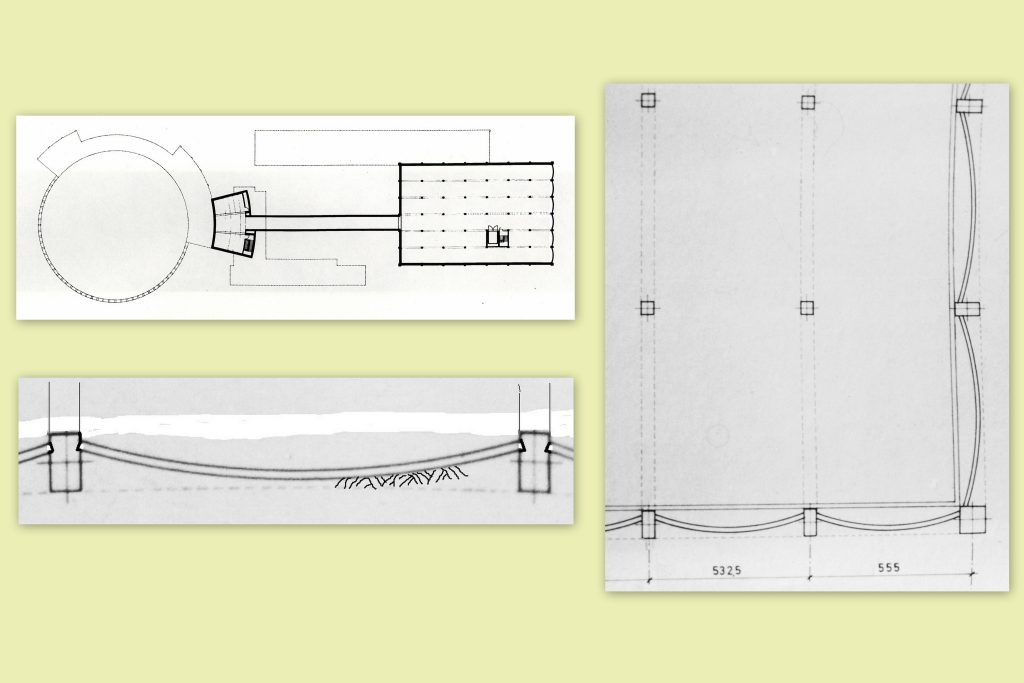
Figura 16.

S’hauria pogut mantenir, fins i tot, la mateixa textura vista que a les voltes del sostre, però això pressuposava construir la contenció amb els totxos de 15×30 posats verticalment com si fos un envà amb planta corba. Això no ens semblava massa fàcil constructivament, pels riscs d’accident i d’inestabilitat que comportaria, i, finalment, vam decidir construir la paret de 15cm. de gruix a la manera convencional, aixecant filada sobre filada, i entregant contra els pilars en una entalla vertical practicada prèviament (fig. 17).

Figura 17.

Un aspecte interessant d’aquesta solució el trobem en la necessitat de mantenir controlats els efectes de les empentes de les terres sobre les voltes verticals. Per aquesta raó, es va disposar un sistema de drenatge que eliminaria les aigües de pluja que es poguessin acumular en el trasdós. Això no era complicat, perquè l’excavació de les terres va deixar un cert talús que facilitava les tasques constructives per fer el mur corbat i per disposar-hi el tub de drenatge. Al mateix temps, també facilitava el poder aplicar un tractament de protecció i impermeabilització ala cara posterior de l’estructura ceràmica. Si observem la figura 18 s’hi veu que l’aspecte actual de les parets corbes es bastant tosc. Una primera conclusió: la fàbrica ha sigut molt més duradora que la làmina de impermeabilització. Recordo ara que quan vam construir se’ns va dir que no els molestava que els murs perimetrals poguessin tenir una certa humitat i això va condicionar la utilització d’un sistema protector no massa exigent.

Figura 18.

El traçat d’una catenària exacta que tenen aquestes voltes és possible gràcies al fet de que les empentes de les terres tenen la mateixa intensitat a tot el llarg de la longitud de la peça (d’uns 5,50 m). No seria el mateix si haguéssim fet un recurs possible, consistent en reforçar la planta del mur com es va fer amb els sostres, acabant amb una capa plana de totxo, connectada amb costelles verticals a la catenària (de manera semblant a com ho feien els tabicons conillers del sostre) al final dels pilars-contraforts. En aquest cas (esquema superior esquerra de la figura 19) el repartiment de les càrregues no hauria estat uniforme sobre la directriu de la catenària, sinó sobre un pla ”horitzontal”, com passaria en els taulers dels ponts arquejats.
Això comportaria que el traçat de la volta ideal no tindria forma catenàrica (hiperbòlica) sinó més tirant a parabòlica i, aleshores, apareixerien, si la volta hagués estat projectada amb criteris estrictament catenàrics, els temuts moments flectors, que provocarien tensions de tracció en la volta, amb la conseqüent aparició de fissuració, que malmetria el bon funcionament de la catenària.
Als esquemes de la dreta de la figura 19 si reprodueix la geometria parabòlica del tirant, de la volta o de l’arc quan les forces no s’apliquen uniformement damunt de la seva directriu, sinó damunt d’un tauler horitzontal (en el cas de ponts de carretera).

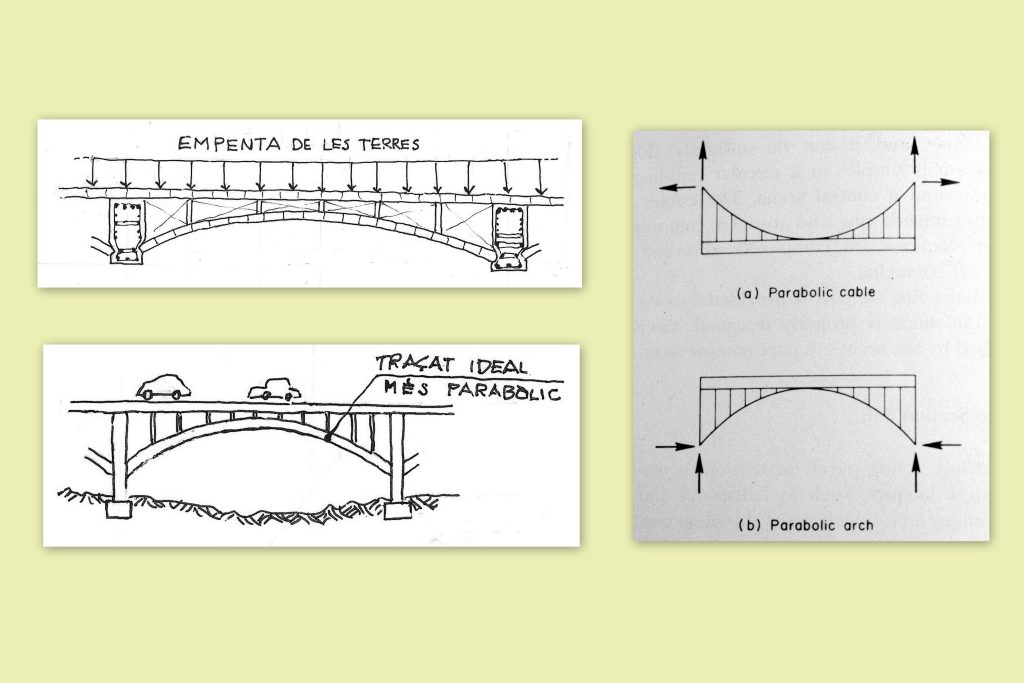
Figura 19.

De quin ordre de tensions estaríem parlant?

Si fem treballar la paret corba a compressió axial pura li haurem de donar forma catenàrica (hiperbòlica), havent d’afinar molt bé la geometria, probablement practicant una inversió, primer empíricament, i després, fent els pertinents càlculs de verificació.
Per tenir un ordre de magnitud anem a fer uns “números grossos”: Suposem, per començar, que hem de suportar les empentes d’un dipòsit d’aigua de 6 metres de fondària. Triem una amplada de 15cm. Donat que l’empenta hidrostàtica comença amb un valor 0 arran del pla d’aigua i acaba amb un valor H t/m2 a la base, voldrà dir que a la franja inferior, entre 5 i 6 m de fondària, sent una mica conservadors, li assignarem una pressió uniforme sobre la directriu de la corba amb un valor de 6 t/ml (fig. 20). La separació entre els contraforts que suporten les parets catenàriques és de 5 m i suposem que sortim d’aquests amb un angle de 20°. Això ens provocarà les reaccions de la figura, és a dir, una força axial de 43’86 en t/ml, que es descompondrien en 15t. en la direcció del contrafort i en 41’21t en la direcció perpendicular.

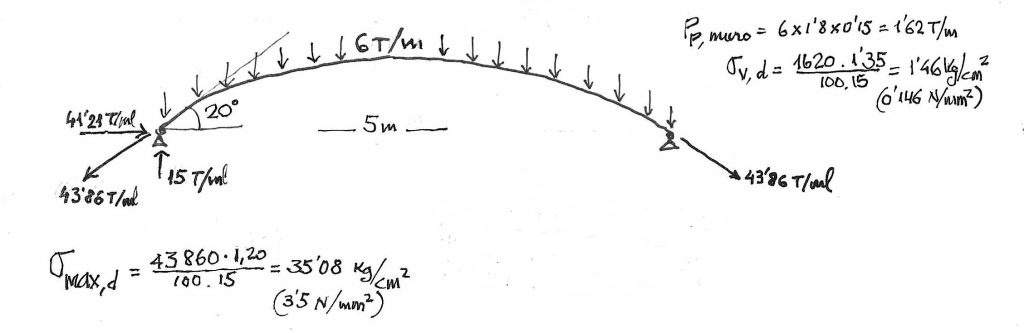
Figura 20.

Majorant les accions provocades per l’aigua amb un coeficient normatiu d’1’20 i les de pes propi del mur amb un coeficient, també normatiu, d’1’35, obtindríem com tensions els següents valors:
a) Tensió horitzontal, en direcció axial:

σh,max,d = 43860 · 1,20 / 100 · 15 = 35,08 Kg/cm2 = 3,508 N/mm²

b) Tensió vertical, deguda al pes propi:

σv,max,d = 6 · 0,15 · 1,8 / 100 · 15 = 1,46 Kg./cm² = 0,146 N/mm²

Són tensions que es podrien acceptar, fent una bona execució de la fàbrica i triant la ceràmica i el morter adequats. Si el primer valor fos una mica major (per considerar, per exemple, una fondària una mica major), hauríem d’augmentar el gruix del mur catenàric, passant, per exemple, a totxo de format castellà, de 12,5+12,5cm de gruix.
A mida que pugem pel mur, les empentes hidrostàtiques aniran sent menors, fins desaparèixer a la cota del pla superior d’aigua.
La component en direcció perpendicular al contrafort (41,21 t/ml) s’hauria d’equilibrar amb les empentes dels trams immediats, construïts amb la mateixa geometria. En el darrer tram hauríem de fer intervenir l’empenta del primer tram de la direcció perpendicular al que considerem, així com les seves empentes passives.

Veiem que per suportar aigua, fent un mur correcte, n’hi hauria prou amb un gruix de 15cm per suportar l’empenta de l’aigua, amb una fondària de 6 m i amb un bon drenatge del trasdós. Evidentment, l’empenta que obtindríem, si en comptes d’aigua suportéssim terres, seria molt menor i el marge de seguretat creixeria molt, amb el mateix gruix de 15cm. No fem els números perquè quan es tracta de terrenys hi ha molts factors i ara ens estem movent en conceptes bàsics.

Si volguéssim afinar el gruix a la part superior del mur, donant el gruix d’un doble envà de totxo massís de 5+5cm de gruix, per exemple, a nivell de càlcul no hi hauria massa problema, però la construcció seria més difícil, i el risc de sofrir algun incident per degradació del totxo o del morter, o per simples actes vandàlics, creixeria, potser innecessàriament.

Si projectem un traçat impecable, la línia de pressions en planta en el mur corb passaria exactament per la directriu del mur, i aleshores no hi hauria excentricitats ni els moments flectors que se’n deriven, quedant molt reduït el risc de sofrir inestabilitats.

Caldria armar el mur catenàric?

Idealment, el mur catenàric no seria necessari que estès armat, ni vertical ni horitzontalment. Ara bé, en determinades circumstàncies podria ser un recurs favorable. Repassem en quines ocasions podria ser convenient.

a) Quan el terreny de base no fos prou uniforme com per no poder garantir que no hi hagués petits assentaments diferencials. Aquesta possibilitat podria ocasionar les típiques fissures inclinades que al produir-se provocarien unes certes discontinuïtats en la paret. Això seria important si el mur catenàric contingués aigua, ja que es produirien fugues no desitjades, posant en crisi la solució. Seria menys greu si es tractés d’una contenció de terres, però, lògicament, la validesa de la solució seria pel cas en que aquests assentaments fossin previsiblement petits. Quan aquesta darrera possibilitat existís, es podria pensar en armar horitzontalment algunes filades, amb barres galvanitzades seguint la directriu, per exemple de Ø8 o Ø10 cada 3 o 4 filades. Aquí estaria bé fer alguns càlculs per decidir aquesta armadura.

b) Quan dos murs catenàrics consecutius no quedessin sol·licitats amb la mateixa intensitat. Això es podria donar quan al trasdós del mur hi haguessin zones immediates que haguessin de suportar sobrecàrregues d’ús molt diferenciades, ja sigui pel possible pas localitzat de vehicles pesats, ja per la possibilitat de que s’hi construís una edificació molt propera que incrementés les empentes. També seria el cas en que el mur no tingués la mateixa altura, sinó que tingués un alçat esglaonat. En aquests casos, per prudència, també es podrien armar horitzontalment els trams afectats.

c) Quan el lloc de l’emplaçament estès en una zona de sismicitat mitjana-baixa (si aquesta sismicitat fos mitjana-alta, aquesta solució no seria adequada). Sempre queda la possibilitat d’armar el mur, tant horitzontal com verticalment. Per que això fos possible, la paret hauria de ser de 15+15 amb els pertinents travaments a l’aparell, utilitzant totxo perforat del tipus que hem vist abans a les voltes del sostre de les caves de Sant Sadurní d’Anoia. La coincidència dels forats entre filades successives faria fàcil aquest armat en dues capes verticals, però aleshores s’hauria de garantir que els forats quedessin totalment reblerts amb morter d’una certa qualitat, per no minvar la capacitat de resistència axial (horitzontal) del mur catenàric.

d) Quan el mur tingués una gran longitud que pogués comportar efectes deformacionals de tipus tèrmic. La forma corba dels murs catenàrics, però, ajudaria al fet que aquest comportament tèrmic no fos massa important.

e) Quan al coronament del mur si hagués d’encastar un forjat, ja que els moments flectors que això podria introduir haurien de ser tinguts en compte.

En aquests casos que hem explicat ara, caldria replantejar-se si fer treballar el mur de contenció a compressió axial horitzontal seria la solució més adequada. Potser, aleshores, el recurs del formigó armat tindria més sentit. Però, encara que hem trobat cinc raons per posar en crisi la solució o, com a mínim, per armar-la, pensem que no són situacions massa freqüents.

En situacions habituals, al territori català, on, si exceptuem algunes zones molt localitzades, no són d’esperar sol·licitacions sísmiques, la solució és possible i aporta avantatges considerables. Es tracta, tot plegat, d’una solució sostenible, que evita, utilitzant criteris saludables d’estàtica gràfica, el consum de grans quantitats de formigó i acer.