Polígon Funicular

JOSEP M. GENESCÀ I RAMON
Consultor d’Estructures.

Comprovació gràfica dels forjats unidireccionals existents¹

ANTECEDENTS

En el número 39 dels Quaderns d’estructures es publicava un article referent a la validació analítica dels forjats unidireccionals existents². A la segona part de les conclusions es deia literalment: «Si el règim en estat actual és l’elàstic, amb o sense lesions, es proposa homogeneïtzar el conjunt d’elements que constitueixen el forjat, tinguin propietats mecàniques o no, i establir l’equilibri aprofitant-se del plus de propietats resistents que tal homogeneïtzació provoca». A continuació, per disminuir la intensitat analítica de l’article abans comentat i facilitar la seva utilització pràctica, es proposa un mètode gràfic, a partir del polígon funicular, per a la validació de forjats unidireccionals existents.

POLÍGON FUNICULAR

Es defineix com a polígon funicular³ d’un sistema de forces o vectors coplanars, un traçat, inclòs en el context general de l’estàtica gràfica, que permet calcular la resultant del sistema, la seva direcció i la seva intensitat.

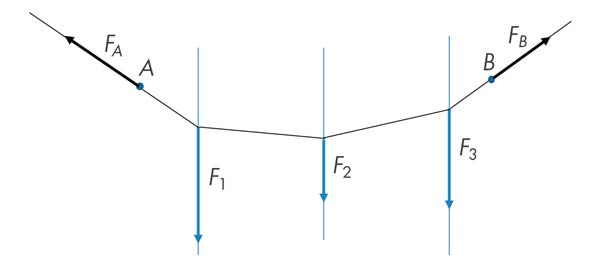
Donat un sistema de forces F₁, F₂ i F₃ (fig. 1) es col·loquen separadament, una a continuació de l’altra, en un polígon que diem de la suma i, prenent un pol qualsevol O, es tracen els radis polars 1, 2, 3 i 4 a una distància polar d qualsevol. Traslladats aquests radis al sistema original, a partir també d’un punt qualsevol A, s’obté el polígon funicular del sistema. Prolongant els costats 1 i 4 del polígon funicular es troba el punt de pas de la resultant R amb una intensitat de valor F₁ + F₂ + F₃.

Si suposem que el polígon funicular és un cordill subjecte en els punts A i B (fig. 2), la forma obtinguda és: 1 (única), 2 (és la que genera la mínima energia potencial), i 3 (és la més eficaç). Les forces F_A i F_B equilibren el sistema.

¹ Aquest article és part d’un estudi més general Polígon funicular. Una aproximació a Karl Culmann del mateix autor.
² «Forjats unidireccionals existents, una proposta de validació analítica». Número 39 de Quaderns d’estructures. Desembre 2010. Josep M. Genescà-Marcel Cruells. ACE Associació de Consultors d’Estructures.
³ El polígon funicular s’estableix de forma definitiva el 1866 a Die graphische Static de Karl Culmann. Karl Culmann neix a Bad Bergzabern, Alemanya, el 1821 i mor a Zuric, Suïssa, el 1881. Enginyer, es va especialitzar en la construcció de ponts i va treballar en el traçat de ferrocarrils. Professor de l’Escola Politècnica de Zuric, comença a donar classes de construcció el 1855. A l’escola explica els sistemes gràfics de Poncelet, de qui es considera el seu alumne, i definitivament anteposa la qüestió gràfica als càlculs analítics. Els mètodes gràfics són més simples i més intuïtius. En el món científic de l’època se li reconeix haver donat a l’estàtica gràfica categoria científica i haver fet que el polígon funicular es pogués aplicar de forma fàcil i operativa.

Els radis polars extrems 1 i 4 generen la resultant R (fig. 3), i les seves paral·leles en el polígon funicular la seva posició. De tal manera que en el polígon de la suma, els radis polars es troben a escala de forces, mentre que la distància entre forces i el propi traçat del polígon funicular es troben a escala de longituds. Podríem dir que aquesta combinació d’escales de forces i geomètriques dona personalitat al polígon funicular.

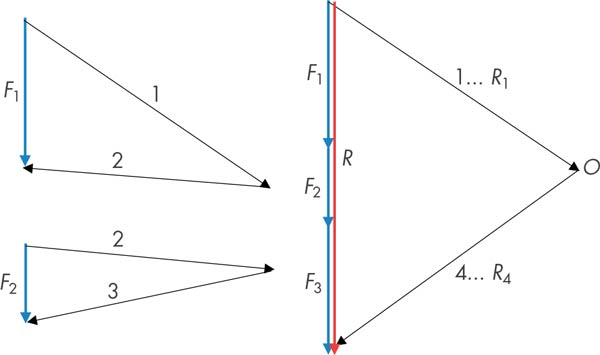
En el següent gràfic (fig. 4) es veu clarament que els radis polars 1 i 4 del polígon de la suma, a escala de forces, es tradueixen en les forces R₁ i R₄ que componen la resultant. Les forces intermèdies del polígon de la suma s’anul·len mútuament (fig. 3), excepte el primer i últim radi polar que, precisament, conforma la resultant. Els altres radis no tenen en el polígon de la suma cap significat mecànic.

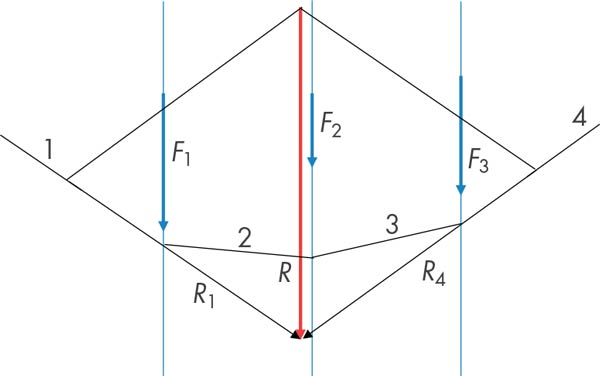
Aquesta qüestió es trasllada al polígon funicular, sent R₁ i R₄ les que componen la resultant R.

De la mateixa manera, en els costats intermedis del polígon funicular les forces s’anul·len mútuament. Per exemple, en el costat 2 (fig. 5). Igual passaria en el costat 3, quedant únicament, com passava en el polígon de la suma, els costats 1 i 4 definitoris de la resultant.

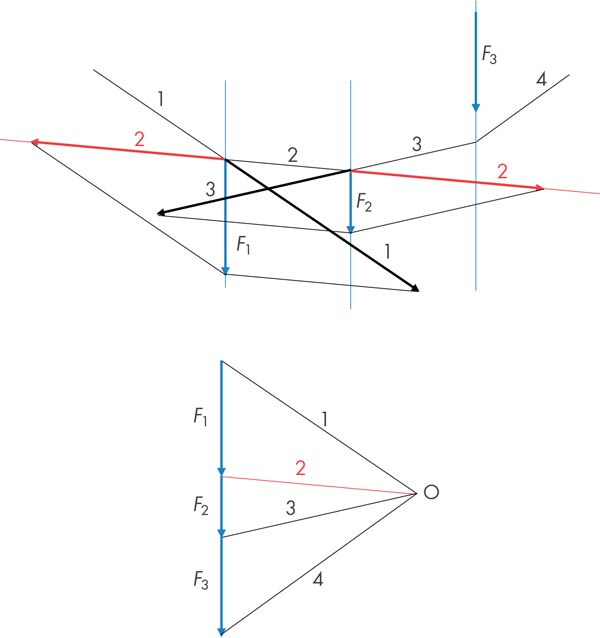
Els criteris fonamentals del polígon funicular, justificant el seu traçat, són els següents:

1. Transmissibilitat. L es forces poden lliscar al llarg de la seva línia d’acció (fig. 6).

Suma de vectors. Es compleix la llei del paral·lelogram enunciada per Leonardo Da Vinci. F₁ + F₂ = R (fig. 7).

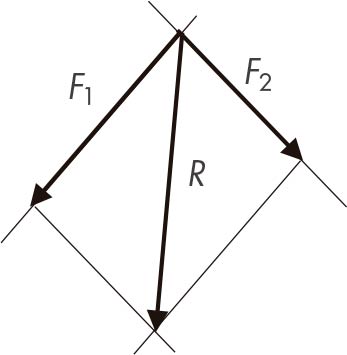
Tercera llei de Newton. L a suma de vectors i la seva resultant estan en equilibri. És a dir F₁ + F₂ – R = 0 (fig. 8).

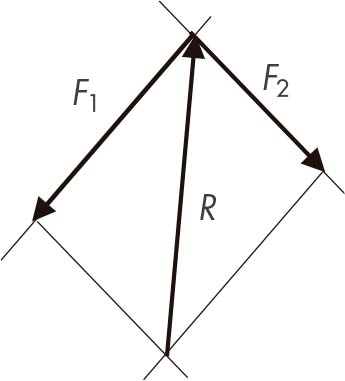
Principi de reciprocitat. Si les paral·leles a les línies que formen un polígon tancat es troben en un punt, es diu que són figures recíproques (fig. 9). Les figures reciproques poden estar en equilibri, però si no ho són, l’equilibri només s’aconsegueix amb l’aparició d’un moment.

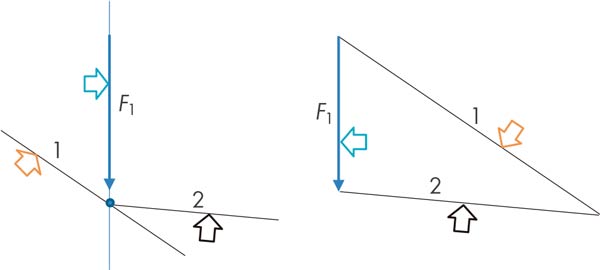
També es comprova que els costats 1-2-3- 4 del polígon funicular (fig. 10) són els recíprocs dels seus homòlegs del polígon de la suma.

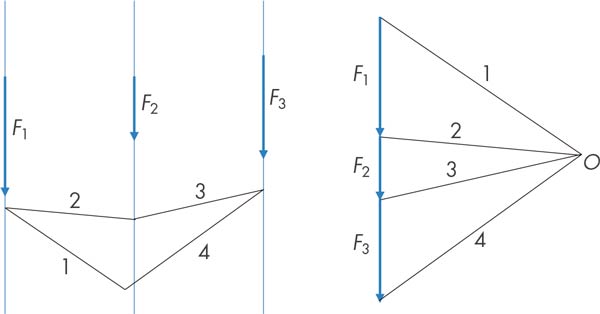
Aquests quatre conceptes permeten enunciar la filosofia en què es basa el polígon funicular: la longitud de cada línia del polígon funicular —forma— representa la longitud de la geometria de l’estructura, i la longitud de cada línia del polígon de la suma —estructura— representa la magnitud de l’esforç axial de l’element de l’estructura amb què està relacionat. Aquesta simbiosi entre forma i estructura (o geometria i mecànica), única en els traçats gràfics i, en particular, en el polígon funicular, es perd amb els mètodes teòrics de càlcul i amb l’ús de l’ordinador, que potencia i facilita precisament aquests mètodes.

FORJATS UNIDIRECCIONALS

S’utilitzarà el polígon funicular per comprovar dos tipus diferents de forjats unidireccionals⁴. En primer lloc, el de ceràmica armada, en aquest cas de bigueta armada, formigonada ‘in situ’ i alleugerit. En segon lloc, el forjat el forma la bigueta de formigó armat fabricada en taller i alleugerit de formigó de baixa densitat. Creiem que no té sentit la utilització del polígon funicular per al disseny o elaboració de les autoritzacions d’ús dels forjats unidireccionals d’obra nova. Hi ha altres formes més exactes i sobretot més automatitzades. No obstant això, sí pot ser convenient el peritatge o comprovació del forjats en els edificis existents especialment per tècnics no avesats en el càlcul. La simplicitat dels plantejaments dels polígons funiculars per definir la idoneïtat resistent dels forjats i l’avaluació de la col·laboració mecànica d’aquells «elements no resistents» com puguin ser la ceràmica en el primer cas de forjat o l’alleugerit o el formigó del sinus en el forjats de formigó. Per tant, en aquest punt s’aprofitarà l’exposició del polígon funicular per comprovar si, efectivament, val la pena la consideració de l’esmentada col·laboració.

⁴ Es pot consultar Recomanacions per al reconeixement, la diagnosi i la teràpia de sostres ceràmics. Ed. Institut de Tecnologia de la Construcció de Catalunya. Victor Seguí – Rafael Bellmunt – Josep Antoni Presmanes. 1995.

COEFICIENTS D’EQUIVALÈNCIA

El coeficient d’equivalència n entre formigó i acer

Amb la utilització del polígon funicular per al càlcul o la comprovació de seccions de formigó armat⁵ s’hauran de tenir en compte diverses qüestions. Fonamentalment, el règim de treball és l’elàstic, és a dir, de proporcionalitat entre tensions i deformacions. Ens situem, per tant, plenament en el mètode clàssic. Per poder dir que el formigó armat compleix Bernoulli, Hooke i Navier s’han de donar unes hipòtesis prèvies que són l’homogeneïtat, continuïtat i isotropia. Com que és evident que el formigó armat no compleix aquestes hipòtesis, s’ha de fer el supòsit que l’acer deixa de ser-ho per a convertir-se en formigó si es multiplica la seva secció per un coeficient d’equivalència n. No es tracta aquí de comparar el mètode clàssic amb altres, més avançats i avui utilitzats, on es treballa amb règims de no proporcionalitat entre tensions i deformacions, però sí seria convenient meditar el valor d’n que s’exposarà a continuació en allò relatiu a l’anàlisi gràfica dels forjats unidireccionals.

⁵ L ’ingredient fonamental resistent en els forjats que es donaran a continuació és el formigó armat.

D’allò anteriorment exposat es dedueix que si alguna utilització ha de tenir el polígon funicular ha de ser en la comprovació de seccions de formigó armat calculades o dissenyades quan el mètode clàssic era l’utilitzat.

L’any 1939 apareix la Instrucción de proyectos y obras de hormigón i després de tres normes intranscendents de 1941, surt l’any 1944 la norma que ha servir de referència per al càlcul en règim elàstic, Instrucción para el proyecto de obras de hormigón. El Instituto Eduardo Torroja de la Construcción y del Cemento publica les instruccions no oficials HA-57, HA-58 i HA-61 i no és fins al 1968 quan apareix l’EH-68 Instrucción para el Proyecto y Ejecución de Obras de Hormigón en Masa o Armado en què s’oficialitzen els mètodes anelàstics. Podem dir que, en general, des de l’any 1939 fins al 1968 es calcula utilitzant el mètode clàssic per projectar i dimensionar el formigó armat.

Seguidament triarem uns materials típics d’aquesta època, tot i que utilitzem la nomenclatura i les unitats actuals, com poden ser: resistència característica del formigó a compressió f_ck = 15 N/mm², i per al ferro el límit elàstic a tracció, f_yk = 420 N/mm², que correspon a un acer laminat en calent i corrugat amb un mòdul de deformació longitudinal d’E_s = 200.000 N/mm².

Definirem coeficient d’equivalència n al valor que s’obté de relacionar entre sí els mòduls de deformació longitudinals de l’acer i del formigó. Intentem quantificar el valor d’n. La Instrucción de Hormigón Estructural EH-08, l’actual, defineix dos valors del mòdul de deformació longitudinal del formigó. L’E_cm, que és el secant als 28 dies, i l’E_c inicial per a càrregues instantànies també als 28 dies. Aquests dos mòduls donen valors d’n (calculant la resistència mitja a compressió del formigó f_cm = f_ck + 8 = 23 N/mm²) compresos entre 7,04 i 8,27. La mateixa instrucció EH-08 defineix els valors reològics a t dies, E_cm (t) i E_c (t). Per a t = 30 anys tindrem els valors d’n compresos entre 6,51 i 7,64. Per tant, la instrucció EH-08 dona valors d’n compresos entre 6,51 i 8,27. Com es veurà, són valors molt baixos en comparació als donats pels autors de l’època.

L’article 27 de la Instrucción de proyectos y obras de hormigón dona el valor n = 2315/R_cub-28 i, en conseqüència, valors d’n compresos entre 7,71 i 15,43.

Les instruccions alemanya, francesa i anglesa de l’època donen el valor n = 15. La instrucció italiana dona el valor n comprès entre 10 i 15.

Per a alguns autors, el valor d’n = 15, ve avalat per Kayser (1931), Salinger (1968)… inclòs P. Jiménez Montoya, que dona valors compresos entre 8,16 i 17,15 i 15 com a allò més corrent. El constructor d’obres català S. Crivillés dona el 1934 valors d’n compresos entre 8 i 15. M. Company dona valors d’n compresos entre 10 i 25. Moral (1962) i d’altres autors no calculen el valor d’n relacionant mòduls de deformació longitudinals, sinó tensions, generalment de trencament. Moral divideix la tensió de 2.400 kp/cm² de l’acer per la de 160 kp/cm² del formigó per obtenir finalment el valor d’n = 15.

Sembla doncs lògic adoptar el valor n = 15.

El coeficient d’equivalència m entre formigó i ceràmica

Amb els forjats ceràmics, apareix un nou material, la ceràmica, que també hem d’homologar al formigó. Per trobar el coeficient d’equivalència m entre la ceràmica i el formigó farem el següent:

1. La Universitat Internacional de Catalunya UIC defineix el mòdul de deformació longitudinal de la ceràmica E_t —referit als maons de ceràmica— com un valor comprès entre 1.000 i 5.000 N/mm².
2. La dificultat d’obtenció del valor d’n provenia, no tant del mòdul de deformació de l’acer E_s = 200.000 N/mm², com de la determinació del mòdul de deformació del formigó.
3. Una vegada optat pel valor d’n = 15 i sent n = E_s/E_c obtenim E_c = 13.333 N/mm².
4. El coeficient d’equivalència m, relació entre el mòdul de deformació de la ceràmica i del formigó m = E_t /E_c , estarà comprès entre 0,18 i 0,38. Adoptaren m = 0,25.

De ceràmica armada

L’exemple que s’exposa a continuació és un cas d’un forjat de ceràmica armada sense lesions. El procés de prospecció i peritatge del forjat serà el següent:

A partir d’una cala⁶, que ha de ser com més representativa millor, s’aixeca una secció del forjat (fig. 11) que essencialment és el que es presenta.

⁶ En general no es disposa d’informació fiable en els documents de l’època en què es va construir el forjat.

Armat inferiorment amb armadures del diàmetre 16 mm i superiorment amb diàmetre 10 mm, en els dos casos amb acer laminat en calent i llis.

A continuació s’aplica el polígon funicular per a l’anàlisi del forjat. Primerament es divideix el forjat en franges horitzontals que hem anomenat A1…A8 i a cada franja li corresponen certes superfícies dels elements constitutius del forjat, modificant tant l’acer com la ceràmica, pels seus coeficients d’homologació al formigó, tal com es veu a la taula 1.

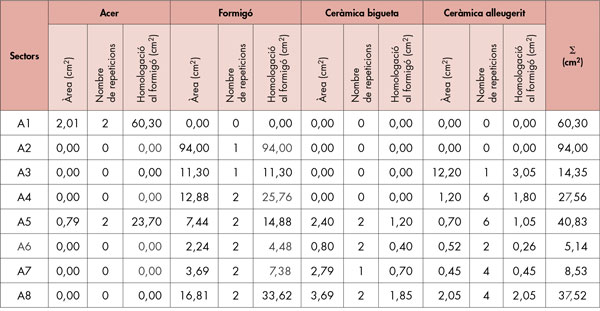
Es munta el polígon de la suma i els dos polígons funicular de pols O i O (fig. 12) assignant a cada vector un valor proporcional a l’àrea de la franja corresponent i amb una distància polar a escala d’àrees de d = 100 cm². S’observa que el vector que representa l’acer a tracció té un signe diferent que els dels altres vectors. La intersecció dels dos polígons funiculars dona la posició de la profunditat de la fibra neutra, de valor x₁ = 5,30 cm i la superfície del polígon 1- …-5-2-1 multiplicat per dos i per la distància polar d ens dona el moment d’inèrcia⁷ I₁ = 7.610 cm⁴.

⁷ Per calcular gràficament, mitjançant el polígon funicular, el moment d’inèrcia d’una figura (o d’un conjunt de vectors que representen les àrees de les franges en què es descomposa la figura) respecte d’un eix, existeixen dos mètodes, el de Culmann i el Mohr. En els dos sistemes es parteix del criteri que el moment d’inèrcia és el moment estàtic del moment estàtic de la figura corresponent.
Si es vol calcular el moment estàtic d’un conjunt de forces F₁, F₂ i F₃ respecte a un punt A, es traça un polígon de forces amb pol O i distància polar qualsevol, en aquest cas d = 50 kN (fig. 13). Prologant els costats extrems del polígon funicular a la línia vertical que passa per A (o amb més rigor, a la línia paral·lela a la resultant del sistema) aconseguirem el segment m-p que, a escala de longituds i multiplicat per d, a escala de forces, ens donarà el moment estàtic de la resultant del sistema respecte al punt A, o el moment estàtic del conjunt de forces respecte al mateix punt, que ve a ser el mateix.
En aquest cas m_A = 302 mkN.
Els triangles m-p-s (on s és el punt de pas de la resultant R) del polígon funicular i el (F₁ + F₂ + F₃) – 1 – 4 del polígon de la suma són semblants. Es dona (F₁ + F₂ + F₃)/d = m p/h. És a dir, que m_A = R · h=5 (F₁ + F₂ + F₃) · h = m p · d. Fàcilment es pot comprovar també que el moment estàtic de cadascuna de les forces respecte el punt A és m_F1 = m n · d … m_F3 = o p · d
Ara tot consisteix en carregar un segon polígon funicular, en què els vectors seran els moments estàtics trobats, i repetir l’operació.

A partir d’aquests valors i amb les resistències del formigó i de l’acer de 18 N/mm² i 240 N/mm² i amb els coeficients de seguretat de 3 i 2 respectivament, obtenim un valor del moment flector màxim positiu d’m = 8,6 kNm.

El polígon de la suma implicava la col·laboració, amb el seu coeficient d’homologació del formigó, de la ceràmica, tant de la bigueta com la de l’alleugerit.

Si es repeteix el mateix traçat geomètric sense la col·laboració de la ceràmica, tant de la bigueta com de l’alleugerit, podrem dir que si és k₁ = 1 la inèrcia en el cas calculat amb la col·laboració de les dues ceràmiques, serà k₂ = 0,97 quan no col·labora la ceràmica de la bigueta i k₃ = 0,95 quan no col·labora cap de les ceràmiques del forjat.

Per tant, en aquest exemple, la consideració de fer col·laborar o no mecànicament la ceràmica fa variar els resultats tan sols un 5%.

De bigueta de formigó

Ara plantegem un escenari diferent que es donava freqüentment a l’època en què situem la present comprovació: no es disposa de la informació d’un forjat sinó d’una bigueta, i en aquest cas de formigó armat fabricada en taller. Efectivament, era freqüent que el constructor adquirís directament al fabricant de biguetes la més adequada per a les seves necessitats, i l’alleugerit a un altre fabricant o esporàdicament al mateix i fos ell qui aportava el formigó o morter de reblert de sinus, obtenint uns elements bigueta, alleugerit i morter d’aportació de sinus que es convertien en un forjat a l’obra (fig. 14).

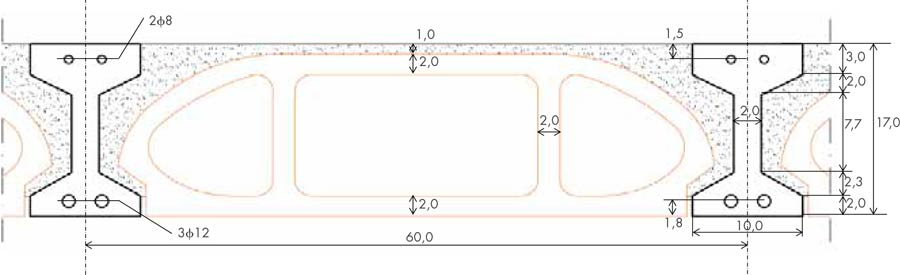
De la mateixa manera que en els forjats de ceràmica armada buscàvem dos coeficients de equivalència al formigó, un per a l’acer (n = 15) i un altre per a la ceràmica (m = 0,25), aquí necessitem uns nous coeficients d’equivalència, el del formigó del sinus i el del formigó de baixa densitat de l’alleugerit. El formigó del sinus pot estar format per un formigó o morter de certa qualitat o per runa de la pròpia obra. No es coneix que el fabricant doni informació de la resistència del formigó de baixa densitat, i molt menys del seu mòdul de deformació longitudinal. Amb aquest escenari, i si es vol fer participar mecànicament a tots (o alguns) dels elements de forjat, s’hauran de donar uns coeficient d’homologació d’aquests formigons altament subjectius extrets de les inspeccions (o impressions) efectuades al forjat que es vol peritar. En aquest cas, si suposem que el formigó de la bigueta, el de referència, té un coeficient d’homologació igual a la unitat, hem considerat que el coeficient d’equivalència per al formigó del sinus és m_s = 0,50 i el del formigó de l’alleugerit m_a = 0,25.

El procés de muntatge del polígon funicular és similar al fet anteriorment per al forjat de ceràmica, és a dir, es divideix el forjat en franges A1…A9 i s’assigna a la superfície de cada franja un vector proporcional (taula 2). Aquestes superfícies estaran compostes per l’àrea pròpiament dels elements compresos a la franja i multiplicats cadascun d’ells pel seu corresponent coeficient d’equivalència.

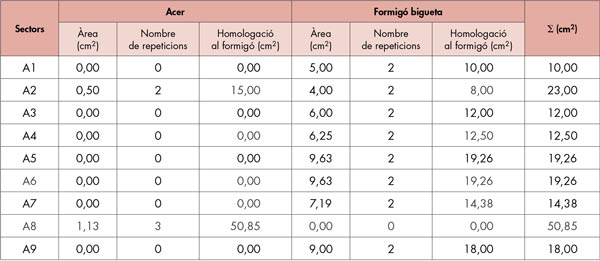
El que sí és diferent en aquest cas és l’ordre d’anàlisi. Per ser conseqüent amb la gènesi del forjat, primerament analitzarem la bigueta i seguidament les repercussions que té el fet de considerar mecànicament el formigó de sinus i finalment el formigó de baixa densitat de l’alleugerit.

La taula 2 designa els valors trobats en els vectors cas que sigui la bigueta l’única responsable del funcionament mecànic del forjat.

Els dos polígons funiculars de pols O i O, amb una distància polar de la qual seguim conservant el valor de d = 100 cm², ens donen uns valors de profunditat de la fibra neutra d’x₁ = 8,47 cm i moment d’inèrcia segons aquesta profunditat d’I₁ = 6.738 cm⁴ (fig. 15).

La màxima compressió en el formigó és de 79,19 kp/cm², i quant a l’acer, la tensió obtinguda és de 943 kg/cm².

Considerant la col·laboració del formigó del sinus tindrem el següent esquema de vectors (taula 3).

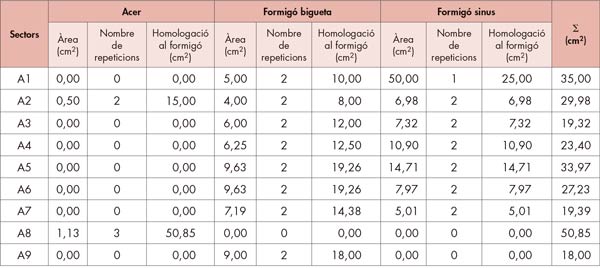
I el polígon funicular corresponent (fig. 16) els valors obtinguts són de x² = 6,66 cm i I₂ = 7.989 cm⁴ amb tensions al formigó a compressió de 52,52 kg/cm² i a l’acer de 1.023 kg/cm².

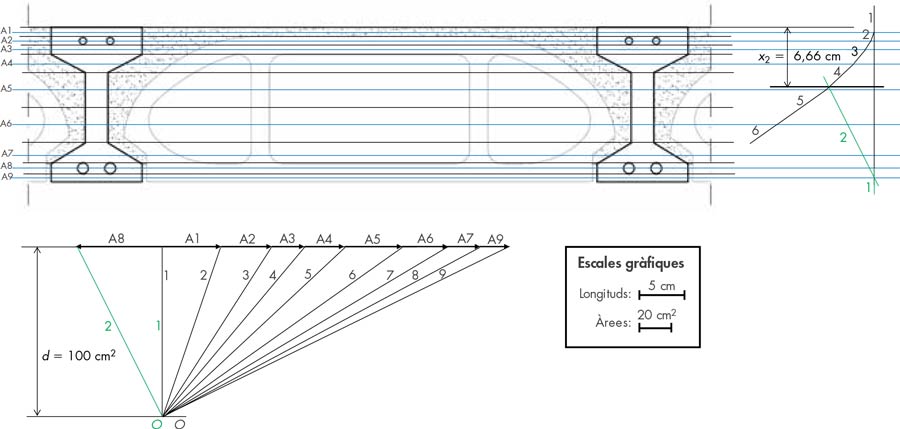
Si considerem a més la col·laboració de l’alleugerit de formigó de baixa densitat, tindrem el següent quadre de vectors (taula 4) i el conseqüent polígon funicular (fig. 17) obtenint x₃ = 6,09 cm i I₃ = 8.325 cm⁴ i tensions de 46,09 kg/cm² per al formigó i de 1.034 kg/cm² per a l’acer.

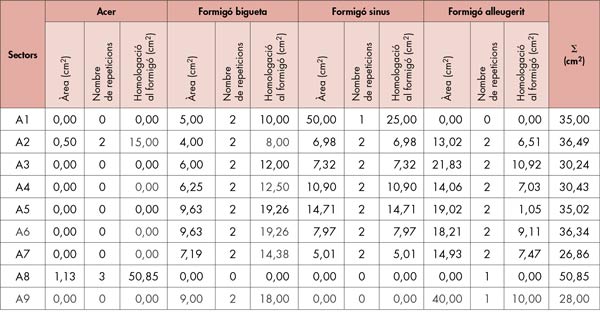
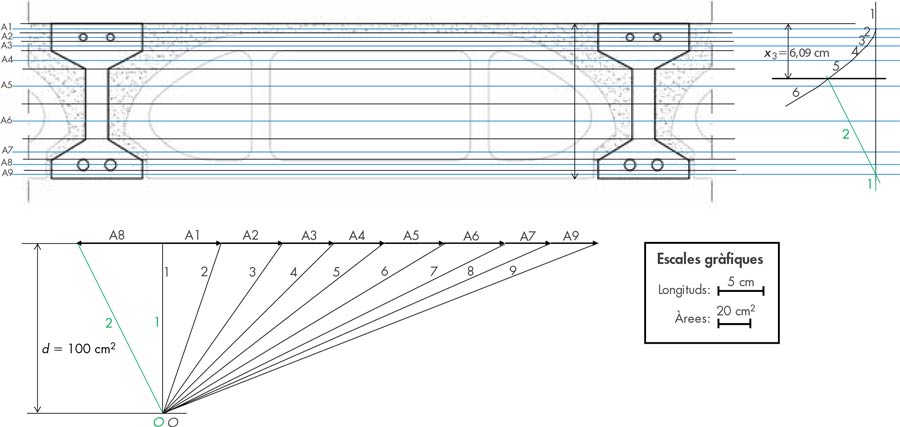
Fem un resum de valor obtinguts amb les tres aproximacions efectuades (taula 5).

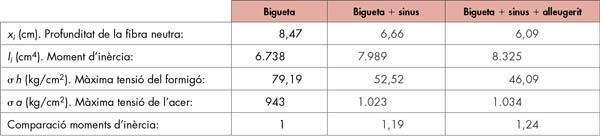
Com a conclusió hem de dir que, al contrari que dels forjats de ceràmica armada en els quals la consideració mecànica de la ceràmica fa augmentar el moment d’inèrcia un 5 %, en el cas de les biguetes de formigó aquests augments se situen en un 20 %, cosa que fa aquesta qüestió molt interessant. Lògicament, perquè aquesta consideració sigui vàlida s’ha de donar una situació prèvia que consisteix en què el forjat no estigui lesionat i, en especial, que no s’observin lesions de falta de compatibilitat o d’adherència entre els elements components del forjat.

RESUM

En aquest article s’ha pogut veure, en primer lloc, que per comprovar forjats unidireccionals existents, dels que freqüentment no es té més informació de la que puguin donar una cala o una autorització d’ús de l’època, és suficient l’exactitud donada pel polígon funicular i aprofitar la seva simplicitat. Amb altres paraules, amb la necessària ubicació del procés en règim elàstic i l’obligatorietat d’homogeneïtzar els components del forjat al formigó, es produeixen més aproximacions que en el sistema gràfic. En segon lloc, s’observa que en els forjats de ceràmica armada no val la pena considerar la ceràmica com a element col·laborant juntament amb el formigó, al contrari que en els forjats de bigueta de formigó, en què la consideració mecànica d’alleugerit i/o sinus poden aportat un plus mecànic d’aproximadament un 20%.